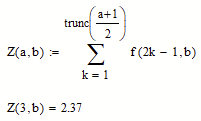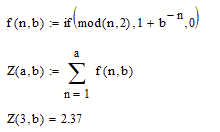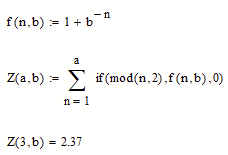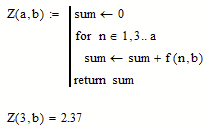Community Tip - Did you get called away in the middle of writing a post? Don't worry you can find your unfinished post later in the Drafts section of your profile page. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Mathcad 15 index summation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mathcad 15 index summation
Is it possible to to index the summation for odd numbers in 15?
- Labels:
-
Mathcad Usage
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Maybe that way:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Or you may redefine your function f(..) to return zero for even values of n:
or, as a variation, you may put the branch into the sum instead of the function f:
And as my last solution for now you may do without the summation operator and program the summation yourself:
The last will not work for a=1 unless you add some kind of branch (if).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I tried to follow the same method in my original programming but the solution does not converge while matlab can
Can you share your views
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You may want to look at the functions An and k_n.
The constant factor in C_b is a quite low pure imaginary number and for most odd values of n the summand is a very small imaginary number , too. But for some odd values of n the summands seem to "explode".
This may also be due to numerical inaccuracies - compare the result of the numeric to the symbolic evaluation shown in the picture for b=21. But both values are quite large so you may want to recheck your function definitions.
There is also a significant difference when I evaluate C_b (for m=41) when evaluated symbolically:
I just noticed that when you define the function An you already have k_n(n,h) in the denominator. When you define C_b you have the same function again in the denominator of the summands. Guess this was not done on purpose?
BTW, you should omit the first argument n in your function definition of C_b as n is the summation index anyway.