Odesolve - in Mathcad 12 OK, in Mathcad 15 and Prime - not OK. Why?

[ValeryOchkov]

Odesolve - in Mathcad 12 OK - see please the picture

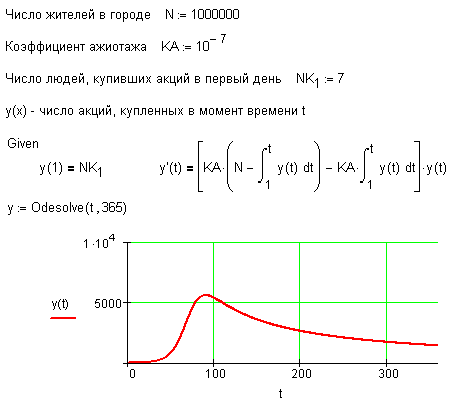
But in Mathcad 15 and Prime - not OK - see please attach.

Why?

[AlanStevens]

Hmmm!  Something odd here Valery.  I've just tried this in my version of Mathcad12 and it doesn't work.  I get the error message: "This definition forms part of a dependency cycle"

Also, the solution I get in M15 (doing it a different way) doesn't look like the solution you provided (see attached)!

Alan

[ValeryOchkov]

Sorry, it was Mathcad 11

See  please this task on Mathcad Application Server 11:

http://twtmas.mpei.ac.ru/mas/Worksheets/FinPyr2.mcd

[AlanStevens · Accepted solution]

Ok.  Firstly, the value of KA in FinPyr2.mcd is different from the one in 15-19-Diff-Int-ODesolve.xmcd! However, this doesn't significantly affect the problem.

Interestingly, in Mathcad 11 it only works if, in the integral, you enter y(t)dt (i.e. you use the same symbol, 't', as for the upper limit).  It doesn't work if you enter y(tau)dtau, say, where tau is a different symbol from the 't' used as the upper limit!  It also doesn't work if you define the integral (using either y(t)dt or y(tau)dtau) as a function before the solve block (say f(y,t):= integral stuff) and replace the integral within the solve block by f(y(t),t). 

It looks to me as though the MC11 "solution" is incorrect!

Alan

.