- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Parabola and catenary
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Parabola and catenary
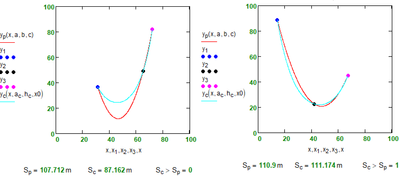
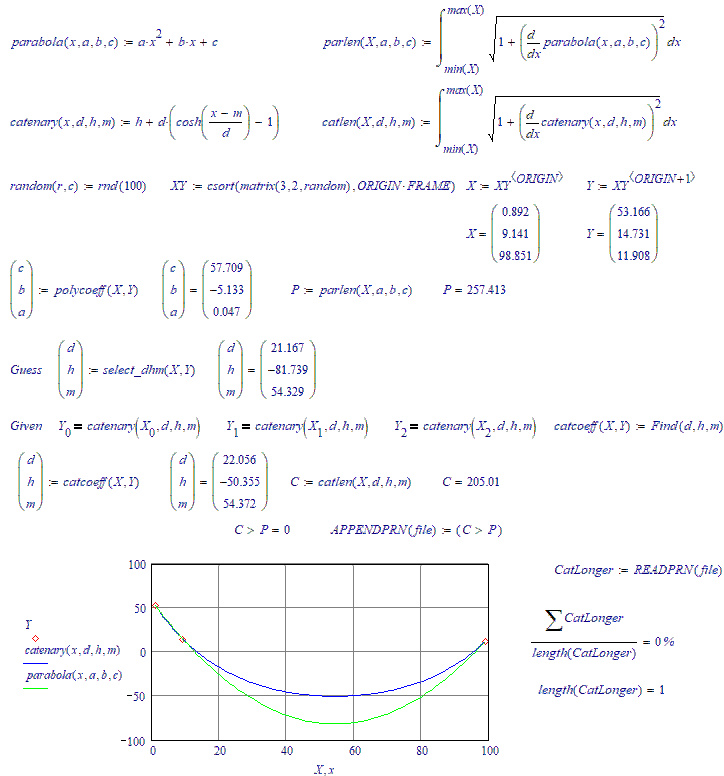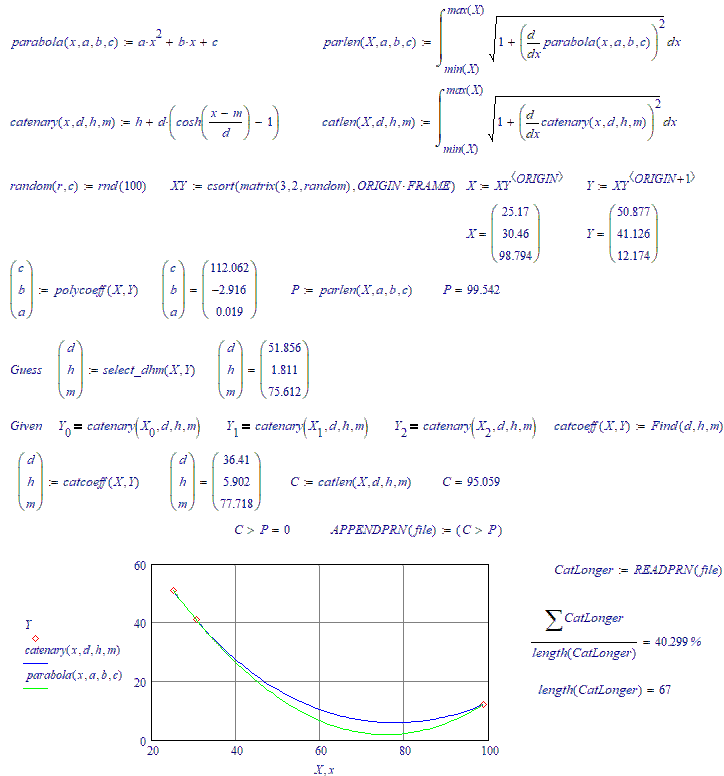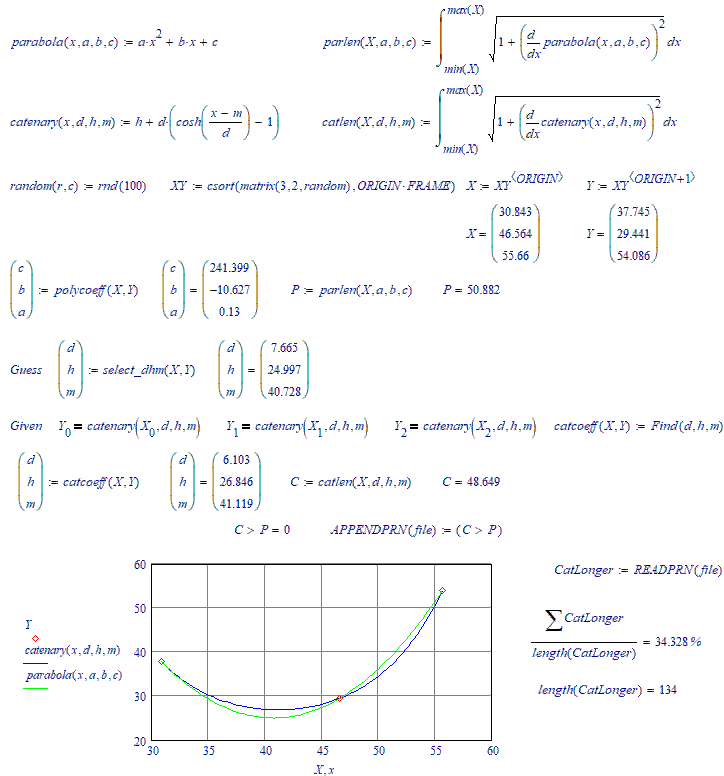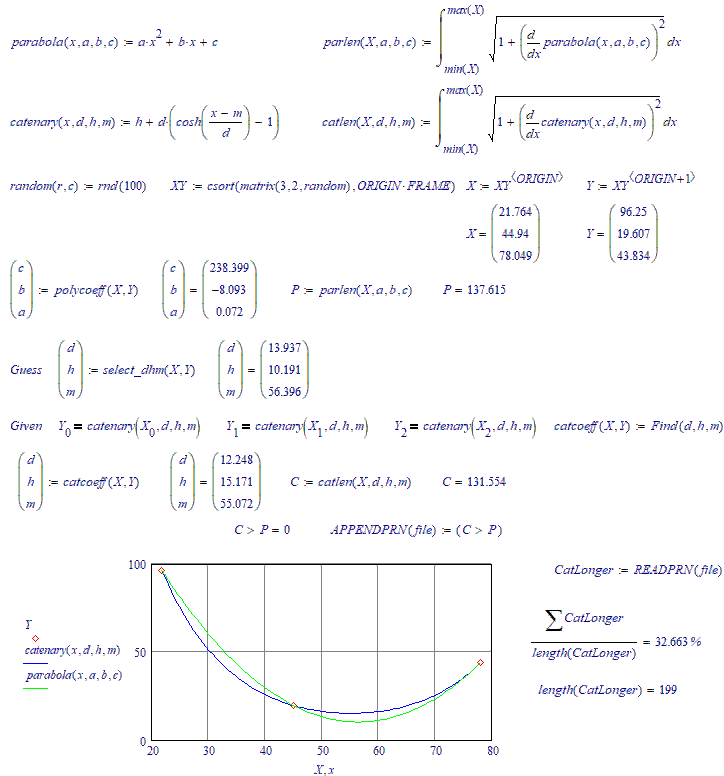
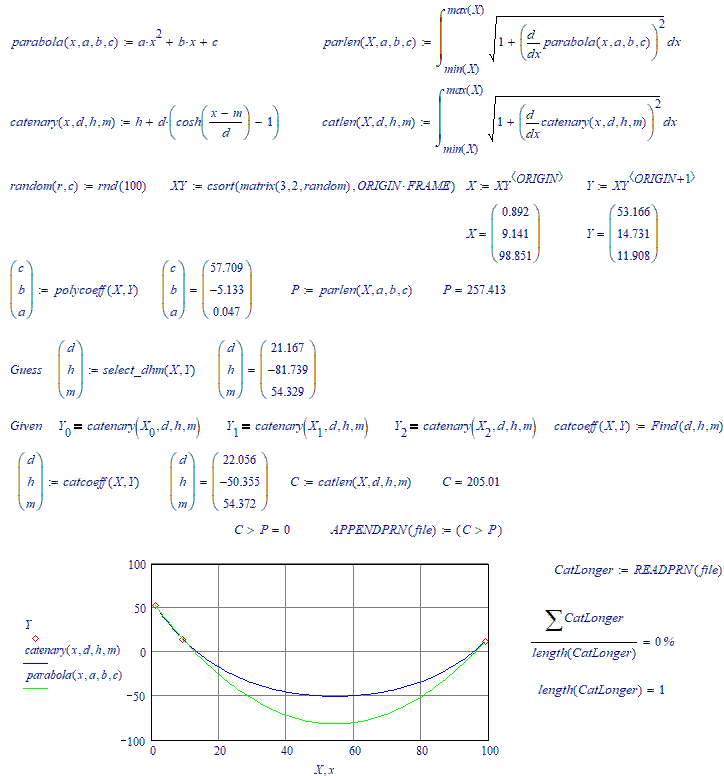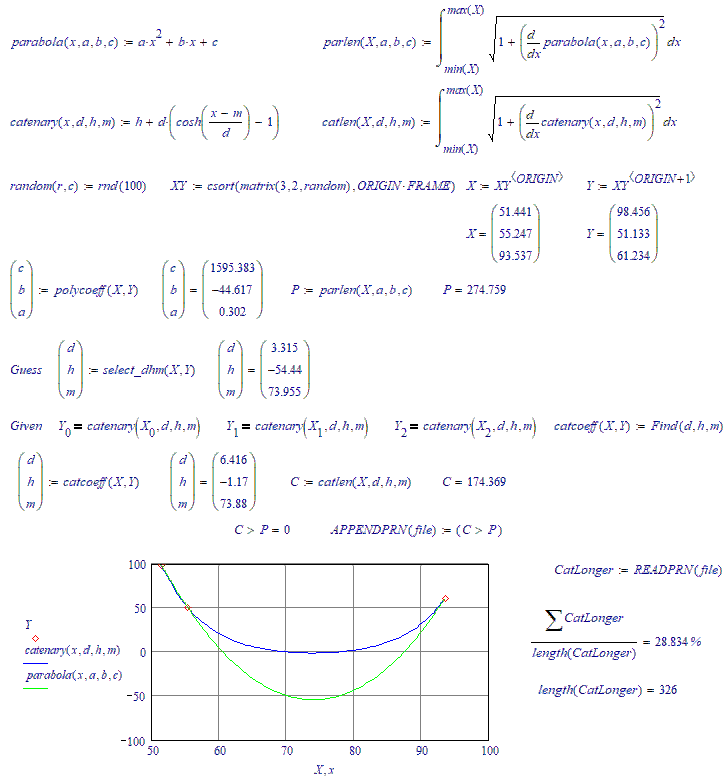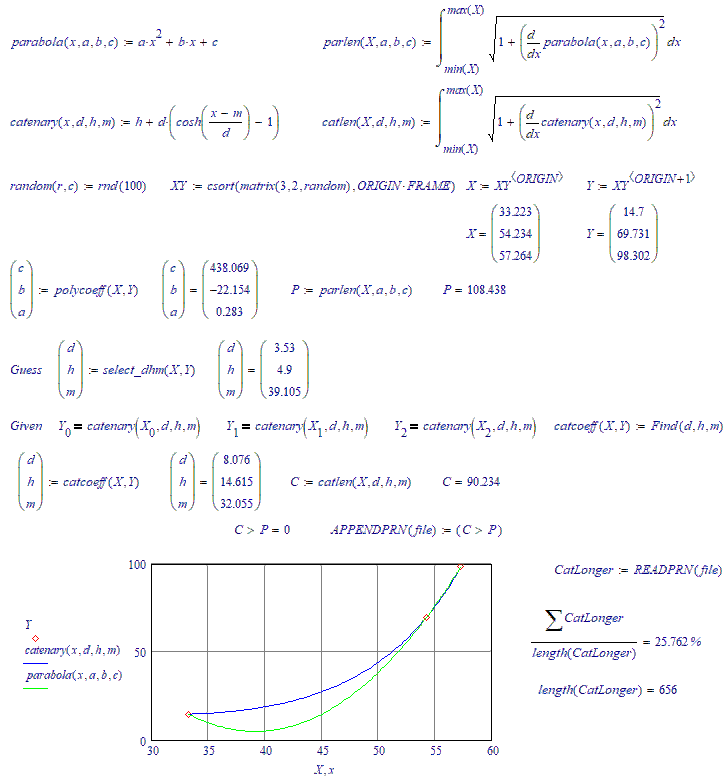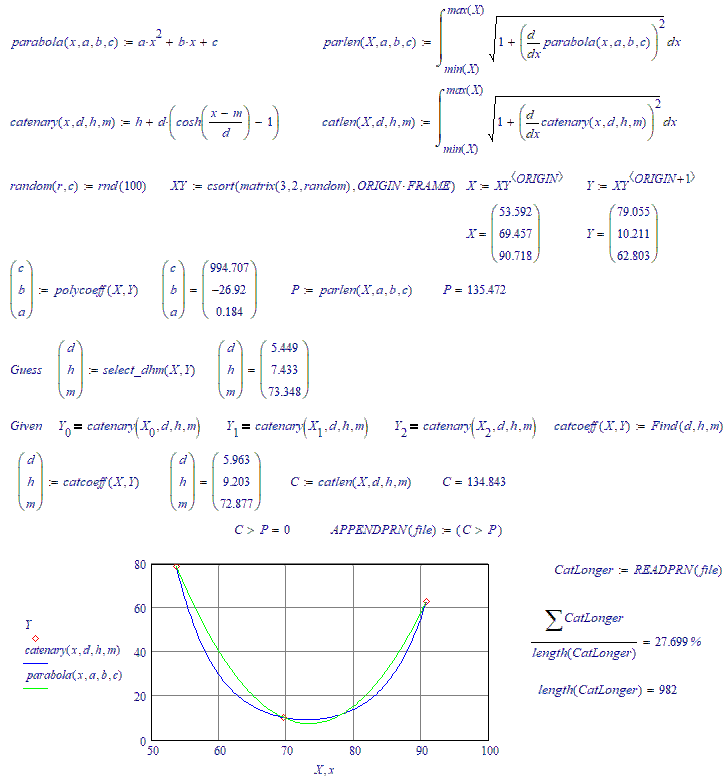
There are three random points on the plane through which an arc of a parabola and a similar arc of a catenary pass. What is the probability that the length of the parabola's arc will be greater than the length of the catenary's arc??
- Labels:
-
Calculus_Derivatives
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Since a catenary describes a condition of minimum potential energy, I would guess that the probability is quite low.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
About 20...25 %.
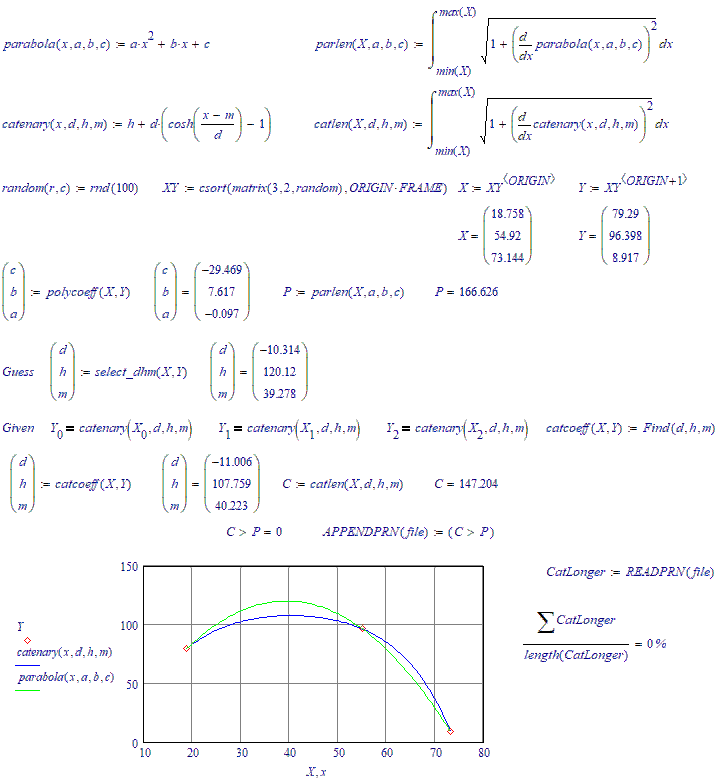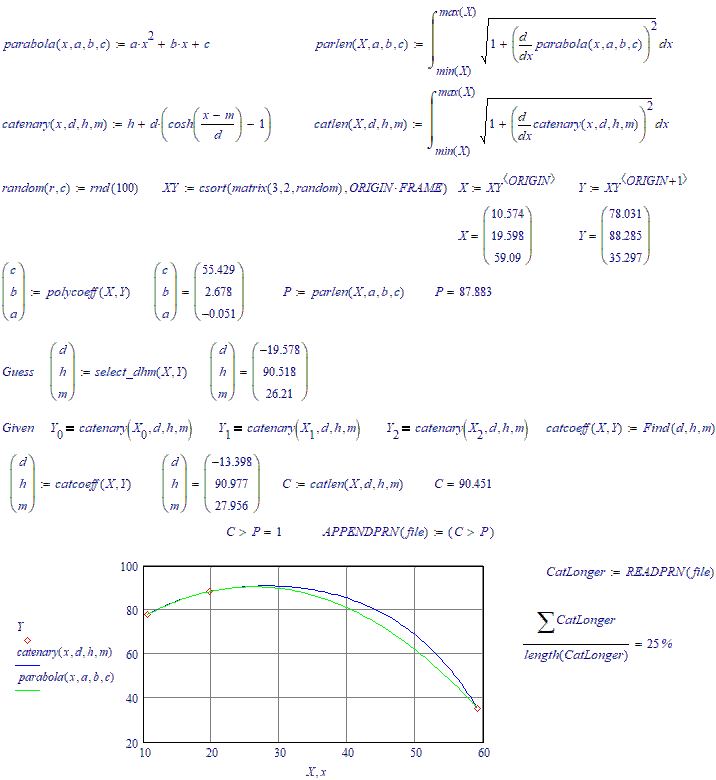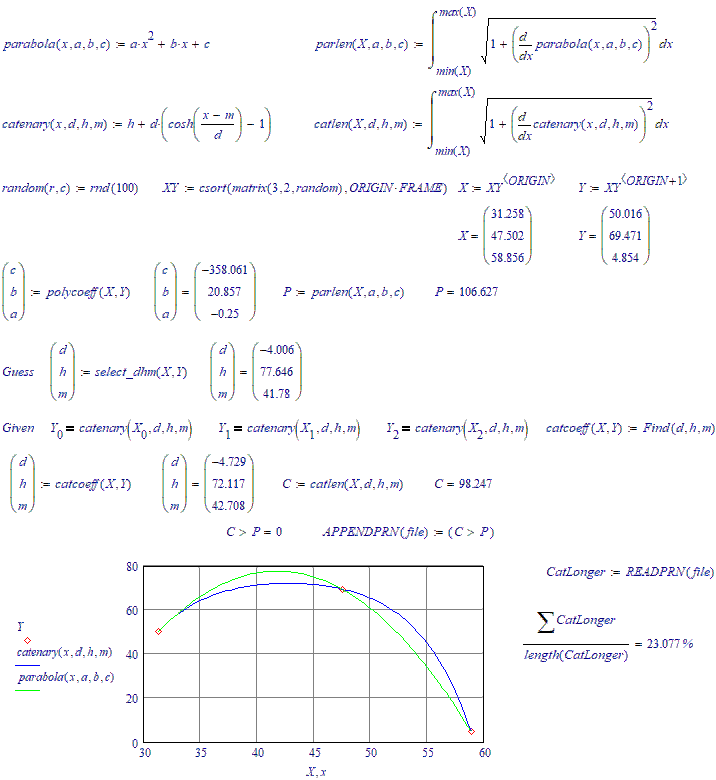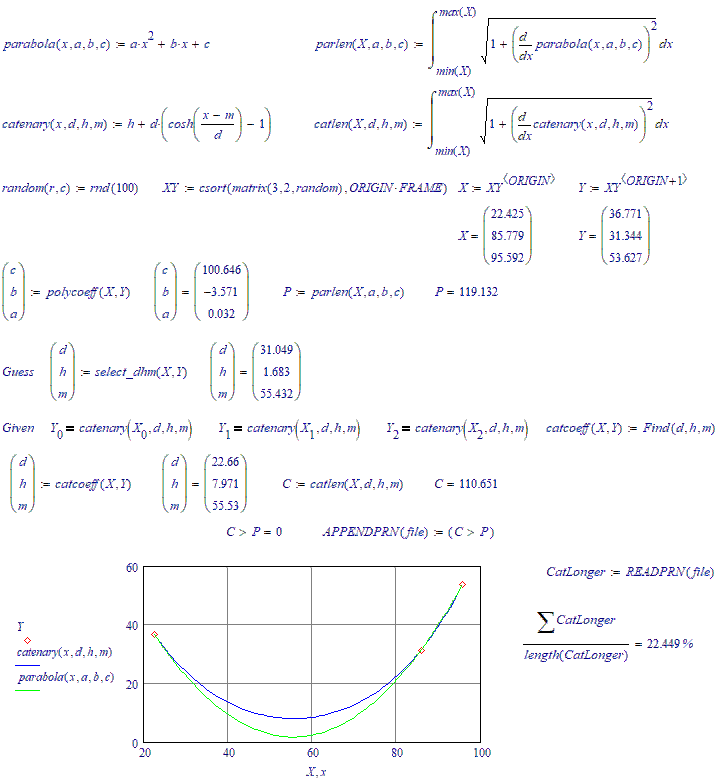
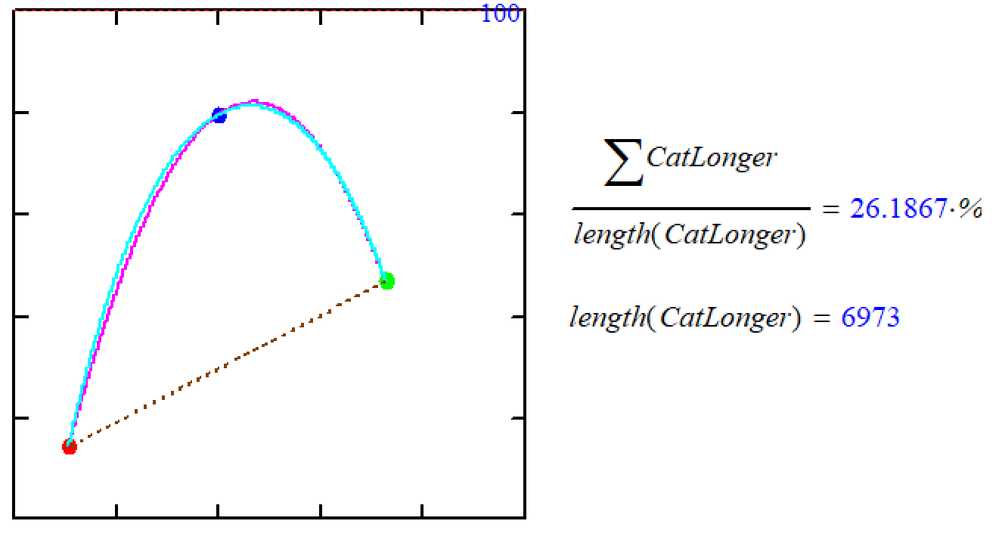
No, it's more towards 30 %. The next run is over 200 iterations:
And finally over 1000 iterations, but showing only 1 in 5:
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Is this a new math constant?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Nah... don't think so.
You would have something if you could prove that a catenary line through 3 points is always x % longer than a Parabola line through the same three points. Since that is not the case....Keep searching.
I've got a puzzle for you: try to find what my select_dhm() function is... (The function I use to provide guess values for the solve block of finding the parameters for the catenary function)
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
what my select_dhm() function is...
rnd, error and cycle?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
No, it's not trial and error. I have an algorithm (a simple formula) that spits out a single set of guess values, with a success rate of over 99 % (that using those guess values, the solve block will find the catenary function parameters. If you look carefully at the animations, you can see the miss shots every now and then...).
That's better than a Covid19 vaccine...
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Rnd, on error and cycle (trial and error) - 99.999%
That's better than a Sputnik V vaccine...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
000100000100010000-0000011010000-00---110000100010000100-011001-0101101-01100000--1101--110101-010-010000101-001-010-0-0001-1-00000--0-10011101000-0-0-00-01010000-0-01-10-0001000-010100-0-00001101011100000110110111--0101-01-101010---000000001000100-000001100111000-10 (Tomorrow I will continue my research)
1 - Sc > Sp
0 - Sc < Sp
- (hiccup) - no solution
* - Sc = Sp (I am waiting for)
It's like a hiccup. You don't know when you will hiccup next time - when next time there will be no solution of the problem of catenaries and parabolas.
By the way, there is a very interesting study of the frequency and strength (- or ---) of hiccups.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Catenary longer than a parabola about (a bit more) in 26 cases out of a hundred.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator