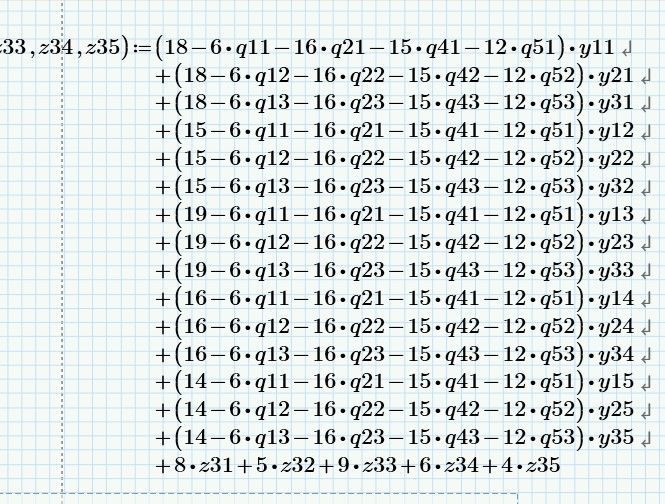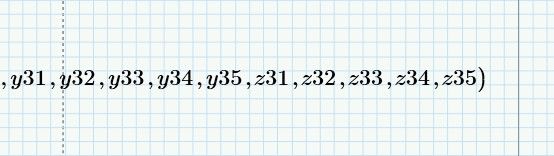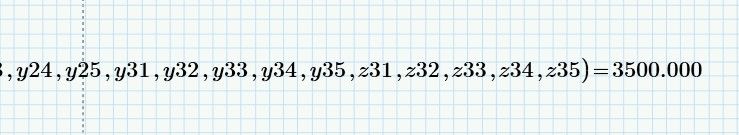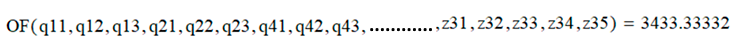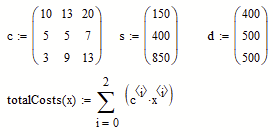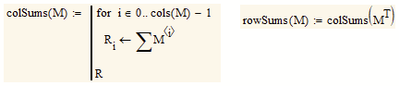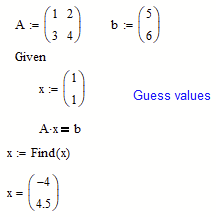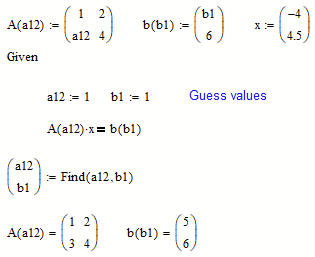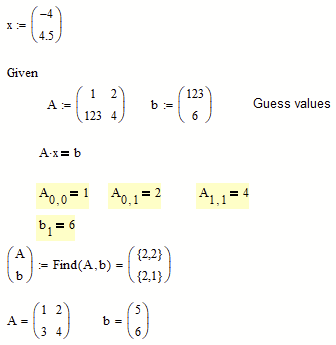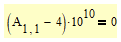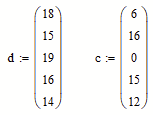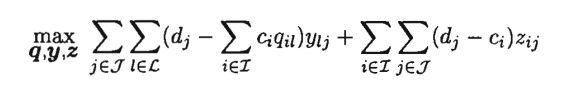Community Tip - Learn all about PTC Community Badges. Engage with PTC and see how many you can earn! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Pooling problem optimization
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Pooling problem optimization
Hello Community,
I have the following task to solve and i dont know how to do it. I guess its just possible with programming well maybe someone can help me.
In the attached sheet i have a pooling problema optimization.
Could anybody help me to find coding to solve pooling problem optimization using Mathcad?
Thanks in advance
Greetings
CarlosRomero
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,'
A better response is gained if you try first then we help.
To get you started look up solve blocks in help.
For the solve block you define the objective function in terms of the 32 variables,
Guess the values of the 32 variables in the guess section of the solve block. I suggest you use the middle of the range of each variable as a start
Set up the constraints in the constraints part of the solve block including the 32 variable range constraints.
Use the maximize function in the solve part of the solve block with your objective function name as parameter plus the list of 32 variables.
There is a video in the Prime help on "maximize" as a search term that will explain in more detail.
Cheers
Terry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
Enclosed Prime 9.0 file. Gets the correct 3500.000 objective function value but with different values than the example.
This could be a different answer with different guess values to start.
You can check the equations.
Cheers
Terry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello Terry,
I am working with Mathcad 15.
Could you attached in M15?
Thanks.
CarlosRomero
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
It is not possible to back save to Mathcad 15 from Prime 9 at the present time.
I am not typing it again.
Enclosed is a pdf printed in A4 landscape.
Some of the maths spills over the page width and this cannot be printed in Prime,
These wider bits are in the three pictures below
Cheers
Terry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I wrote your sheet in Mathcad 15, but something seems wrong.
Greetings
CarlosRomero
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello friends,
I can´t get the value 3500 wiith MC15. Maybe I have to modified initial values or TOL or CTOL?
As you can see in the picture below, I can´t get the value 3500 wiith MC15.
I also want to ask you, if it is possible to simplify the problem using summations as this class of problems is defined? As in the image presented.
Thanks in advance for any help.
Best Regards,
CarlosRomero.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
I expect the equations still have an error if not getting the 3500, so need to check them.
Cheers
Terry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Like Terry I also can imagine that you still have typos in your sheet. Sure not easy to spot (the double occurrence of q12 was easier to spot) and you would have to very carefully compare Terry's pdf of Prime and your Mathcad sheet.
And yes, it might(!?) be able to write the objective function and the constraints and bounds in a more clear way using matrices.
You would first have to define the matrices whose values are know and provide guess matrices for the unknowns.
It also might be possible that its necessary to write some auxiliary function to deal with he various sums in the constraints as you can't use range values in he solve block.
In the example in the other thread with
the approach using ranges i and j does not work
If trace back that error you land a t the i in the sum at the column selector <i>.
Thats the reason I had to define auxiliary functions
to be able to formulate the constraints
Furthermore it looks to me (had not looked in detail at the example in the pdf you attached) that in your new example some values in the matrices are already predefined (maybe zero, as they do not occur in the schematics) and must not be changed and some are to be looked for. This also can be tricky.
While its possible to let a solve block find whole matrices or vectors if you provide appropriate guess values like in
it can be tricky if just part of the matrices are unknowns and it might be necessary to define some of the matrices as functions similar as seen in this simple example
Another approach which avoids defining the matrices as function would be to add additional constraints for the matrix elements which should be constant
In case of a maximisation task it may be necessary to "weight" those constraints which could be done by using something like
So as a conclusion: Yes, maybe it could be done, but it can get tricky and more difficult than you may expect at first. Quite some work to do.
First step would be to define the vectors and matrices d,c,A,S,D,C and P which are not given explicitly in the pdf you posted and may just be deducted from the given constraints like
Next step is to determine what the dimensions of the vectors/matrices q (5x3), y (3x5) and z (5x5) would be and which elements of these vectors must be set to constant zero. E.g. q31, q32 and q33 must be constant zero because there is no connection from feed #3 to any of the three pools. Likewise only row #3 in z is non-zero because feed #3 is the only feed with direct connections to the five products.
And now you would have to either define those three marices q,y,z either as fnuctions as shown in the example above or add the zero values as additional constraints.
Now try to formulate the OF and the constraints and limit using the summation operator similar to the formulas given in the pdf - you may have to make use of auxiliary functions as described above and shown in the other thread.
Good luck!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Additional remarks according the OF not yielding 3500:
- Yes, the setting of CTOL affects the result, but probably only slightly
- Yes, the choice of the guess values may (!) sometimes have a massive influence on the result. No idea if that's the case in your example. Simply give it a try.
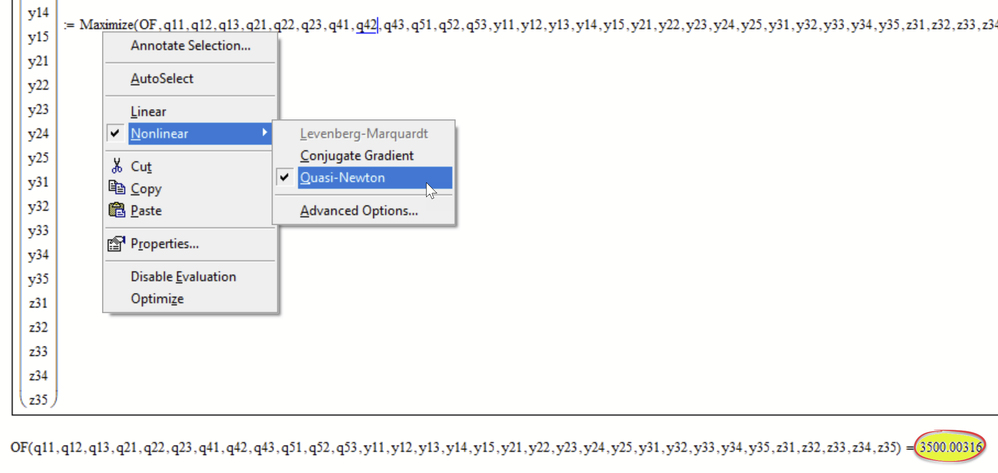
- The algorithm used in the solve block will have quite some influence. Prime uses different algorithms (KNOVEL) than Mathcad. In Mathcad you have a choice (right click the word "Maximize") and you can also set some option. Default is for non-linear problems the "Conjugate Gradient" algorithm which also usually is the best choice.. If I change it to "Quasi-Newton" i get this:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi
Werner, Carlos
Spotted the constraints should be 200 for these values where sheet has 100.
Cheers
Terry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
Have converted the optimization equation to the matrix form using summations as per the document. Now going to do the constraint equations in the same way I hope.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Excellent, Terry.
It´s more clear.
CR.