Community Tip - Did you get an answer that solved your problem? Please mark it as an Accepted Solution so others with the same problem can find the answer easily. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Portrait of roots of two equations
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Portrait of roots of two equations
I announce a competition - who will create the most interesting and beautiful portrait of the roots of two equations. I will send a hard copy of my book (2⁵ Problems for STEM Education - 1st Edition - Valery Ochkov - Rout (routledge.com)) to the winner of the contest. The end date of the competition is April 1, 2022. I will personally determine the winner. Materials explaining the essence of the task, in attachment. In the picture - a sample of a work of science and art, which should be submitted to the competition.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Russian avant-garde of the early 20th century.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sankt-Peterburg
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Our paintings will look good in a house where the wife is a designer and the husband is an architect.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
ValeryOchkov wrote:
Our paintings will look good in a house where the wife is a designer and the husband is an architect.
:-D)
I wonder wher you take all those pictures from 😉
Lets see how you are doing playing around with my sheet. Maybe you can find some interesting position where its worth to zoom in or some nice color sets.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I hope this case will be interesting (2 roots)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ValeryOchkov wrote:
I hope this case will be interesting (2 roots)
Maybe. Will also depend on the center position and the zoom factor, I guess.
Give it a try and show the generated art work.
BTW you were cheating in the plot you showed - lemniscate and oval aren't even touching on close look.
The scaling factor needed for the lemniscate would be 1/2* sqrt(3).
EDIT: I just notice that I already posted the picture showing exactly the case of touching oval and lemniscate -> https://community.ptc.com/t5/PTC-Mathcad/Portrait-of-roots-of-two-equations/m-p/778067/highlight/true#M199817
There is not much difference compared to the case with four points of intersection other than only two colors (plus black for "no solution") are used instead of four.
Anyway, I recreated the pic and included it in the small gallery below.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here some more galleries. Combining multiple curves results in more points of intersection and more colorful pictures.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fine!
But what is it?
Or so
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ValeryOchkov wrote:
Fine!
But what is it?
What it is? I would say its off-topic because its not created by Mathcad but edited using a paint program and because it does not follow your initially stated requirement "portrait of the roots of two equations" using the effects of a numerical algorithm. 😄
But of course we could use the equation you show to create on-topic pics:
or a bit simpler:
The latter contains a lot of black (no solution) in the center and this does not change when we switch from LM to QN:
Here are a few more on-topic pics 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The best
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ValeryOchkov wrote:
The best
I remember that I pressed F9 many times on the expression to change the random color until I could claim it to be the pic of a flower 😉
There are 16 point of intersection and no positions where there is no solution. So the image consists of 16 colors. Here are a few other random colorings of the same picture:
But the pictures that consist of fewer colors also have their appeal. For example the following - has something of Lost in Space.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
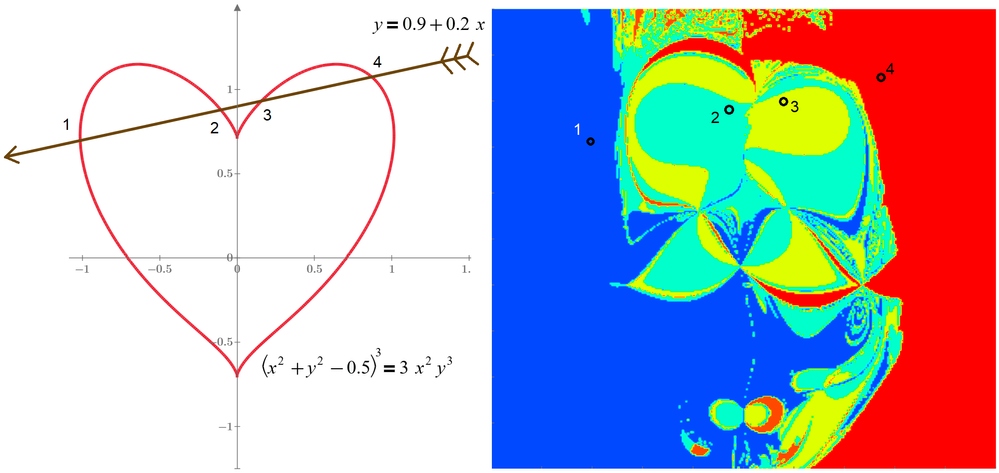
The key to the secret of the mystical face is the partial derivatives of the heart.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I have find in internet same portrait
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Chaotic behavior in an algorithm to escape from poor local minima in lens design (optica.org)
See color pictures in this article
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I propose a sketch of a tattoo - one of the faces of the goddess of mathematics Athena - the face of applied mathematics. An applied mathematician or programmer can come to a tattoo salon and order such a tattoo on his body.
And speaking seriously, we can say the following.
The theme of the portrait of the roots of a system of two equations is presented in the first chapter of this book.
STEM Problems with Mathcad and Python - 1st Edition - Valery Ochkov - (routledge.com)
Go to the site and order not a tattoo, but the book itself 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The article on this problem
See the attach
One part of the article.
Thanks, Werner, onr more! I have a dream to be your coautor.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
SMath: the built-in faction roots vs the user function Newton
- « Previous
-
- 1
- 2
- Next »