Community Tip - You can subscribe to a forum, label or individual post and receive email notifications when someone posts a new topic or reply. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Using minimize for a function which depends on parameters
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Using minimize for a function which depends on parameters
Dear helpers,
I am quite new to Mathcad and have the following question using the minimize optimization in Mathcad15.
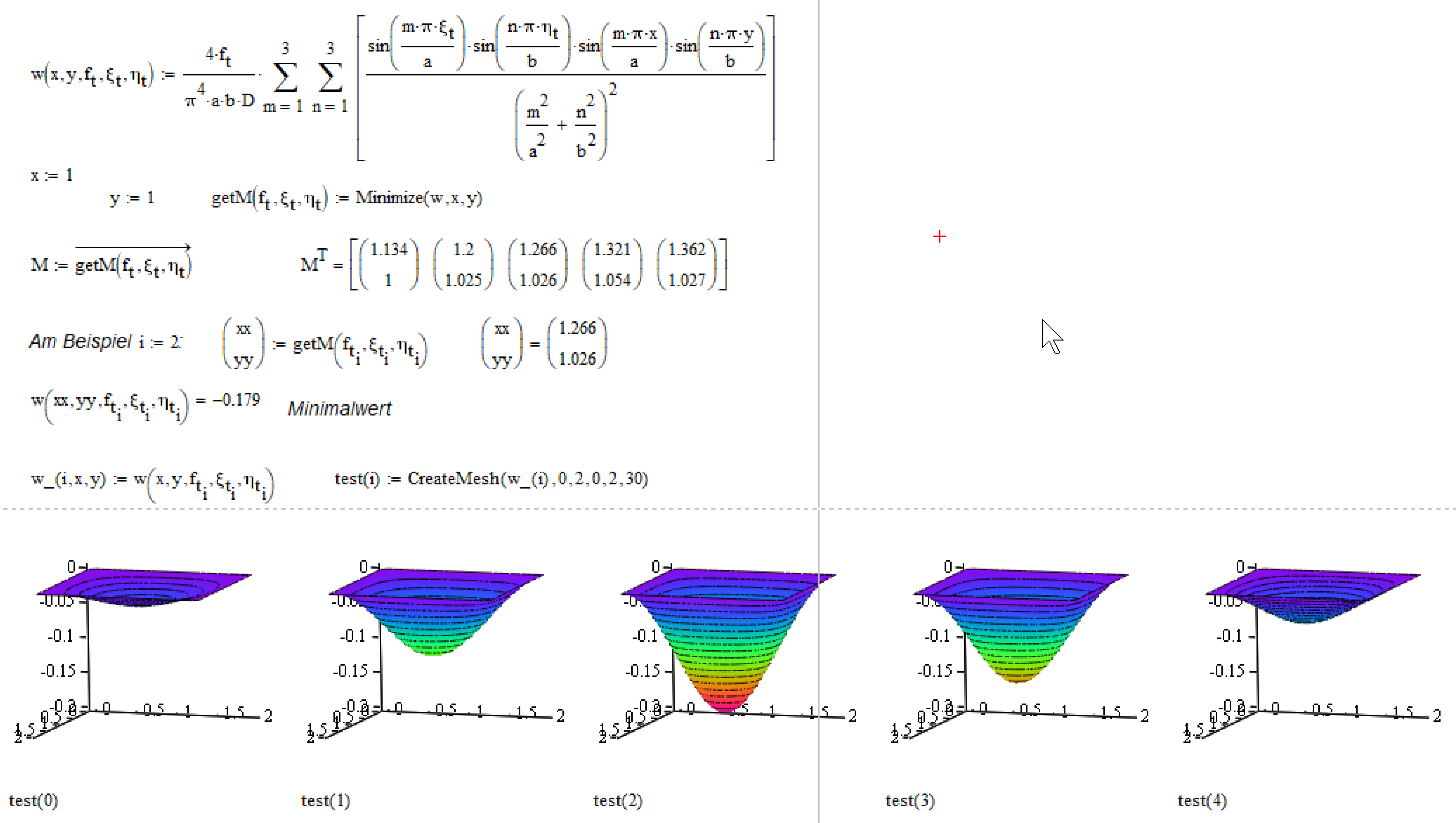
I would like to calculate the maximum of deformation of a loaded plate (=minumum of plate equation). Therefor I use a plate equation w(x,y) with several parameters (force and force location (x and y)) for several time steps by adding an Excel component. (Each time step has a set of these three parameters.)
I was able to calculate the minimum for each of these steps seperate but my goal is to use the minimize optimization for w(x,y) dependent on the parameters so that the solution is a vector consisting of the several minimums for each parameter set.
I appreciate any kind of help.
Thank you!
Solved! Go to Solution.
- Labels:
-
Mathcad Usage
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I am sorry, but I have to tell you, that the results you get for a single set of values is wrong.
You ran into a common trap when dealing with vectors.
Short explanation what went wrong: you define a function w(x,y) which uses a couple of vectors (the forces).
You calculate sin(..vector) and this is a vector, as it should be. You do it a second time and the you multiply the two sines. That means, thats you multiply two vectors and Mathcad does as commanded and if you multiply two vectors, Mathcad uses the dot product and the result is a scalar. Not what you intended. The whole double sum simplifies to a single scalar value which is then multiplied by the result of the expression in front of the sums and this is a vector, so the whole result is a vector and it looks like all was done as you expected - it wasn't.
A way out could be to use a Mathcad feature called vectorization (the arrow over an expression). If you multiply two vectors and use vectorization, the vectors are multiplied element wise. If mathcad encounters an operation which is not defined for vectors (like sin(vector) or vector^3) it switches automatically to vectorization (otherwise it would have to throw an error because of an invalid operation).
The main reason for falling in the trap is a wrong approach to the problem by defining the input vectors first and applying them to all calculations (this should work OK if you use vectorization, but its not tge best way to do it). Most of times its better to set up the calc sheet by defining functions which depend on all variables you later wish to change. After calculations are turned into functions you can define your input vectors and call the function(s) with them (but of course you would vectorize that call!).
So you always can test your calc functions with single values and different vectors at will side by side.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I am sorry, but I have to tell you, that the results you get for a single set of values is wrong.
You ran into a common trap when dealing with vectors.
Short explanation what went wrong: you define a function w(x,y) which uses a couple of vectors (the forces).
You calculate sin(..vector) and this is a vector, as it should be. You do it a second time and the you multiply the two sines. That means, thats you multiply two vectors and Mathcad does as commanded and if you multiply two vectors, Mathcad uses the dot product and the result is a scalar. Not what you intended. The whole double sum simplifies to a single scalar value which is then multiplied by the result of the expression in front of the sums and this is a vector, so the whole result is a vector and it looks like all was done as you expected - it wasn't.
A way out could be to use a Mathcad feature called vectorization (the arrow over an expression). If you multiply two vectors and use vectorization, the vectors are multiplied element wise. If mathcad encounters an operation which is not defined for vectors (like sin(vector) or vector^3) it switches automatically to vectorization (otherwise it would have to throw an error because of an invalid operation).
The main reason for falling in the trap is a wrong approach to the problem by defining the input vectors first and applying them to all calculations (this should work OK if you use vectorization, but its not tge best way to do it). Most of times its better to set up the calc sheet by defining functions which depend on all variables you later wish to change. After calculations are turned into functions you can define your input vectors and call the function(s) with them (but of course you would vectorize that call!).
So you always can test your calc functions with single values and different vectors at will side by side.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is a small animation - simply used linear interpolation of your vectors of forces.
I attach the avi-file, too, as its usually more convenient and embedded videos often fail here.
EDIT: As the embedded video still does not work, I replaced it by an animated GIF.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Dear helpers,
thank you so much for your kind help which is the solution for my problem. I appreciate that.
Werner, that is exactly what I was thinking about and I tried something similar before but my results looked unlikely. Now I know it was a wrong vector version and I changed the vector display settings.
Also your animation and interpolation helped a lot.
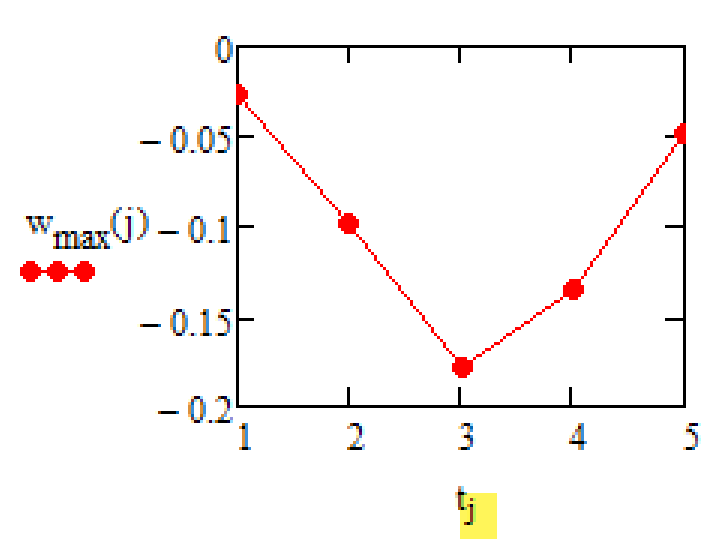
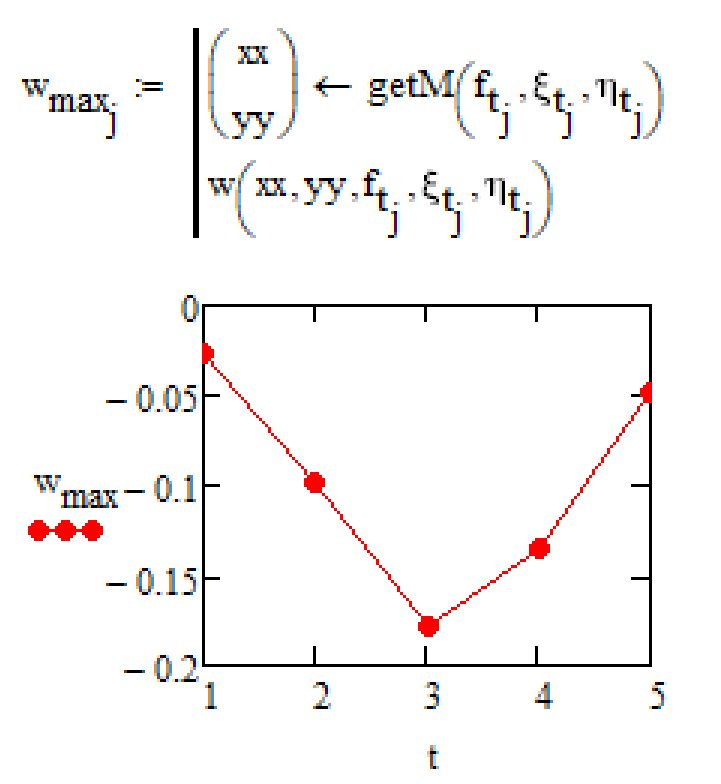
I am now trying to plot the maximum deformation (=minimum of the plate) against the time. I was able to plot it against "j" as FredKohlhepp suggested in his data. "w_max" in this case is dependent on "j", which goes from 0 to 4. Is it also possible to plot "w_max" against "t" from my input data independent on the time steps of "t"? (So that every "w_max" is assigned to one time "t")
Thank you again for your help.
Felix
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Staying with the ranges you could simply do it that way:
Or you could create a vector of all the max values and plot that vector over vector t:
Another option might be to create functions for the forces (by using linear or spline interpolation), create a function which returns the max value and plot that function.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you, Werner. I just forgot the index "j". Sometimes it's that easy 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
So you can test your answers here is another approach for a simply supported plate.
Cheers
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator