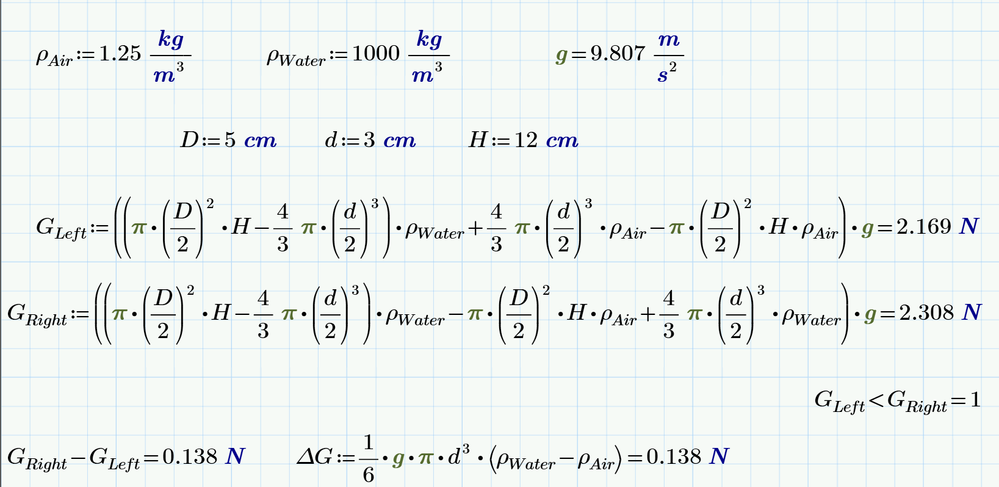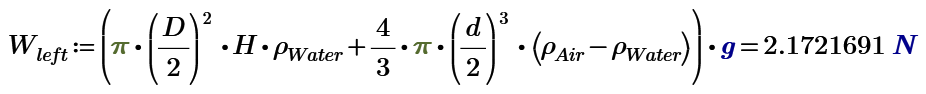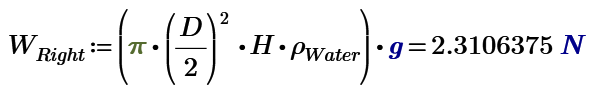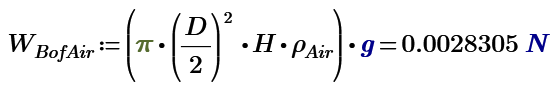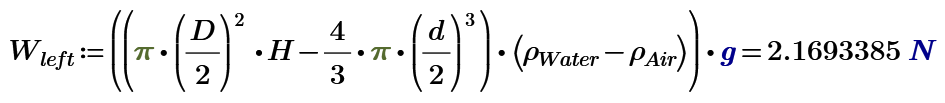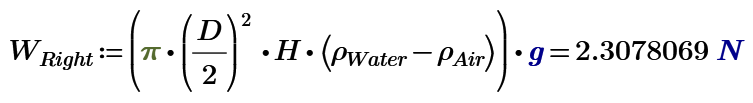- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
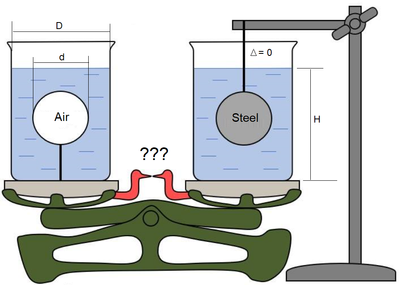
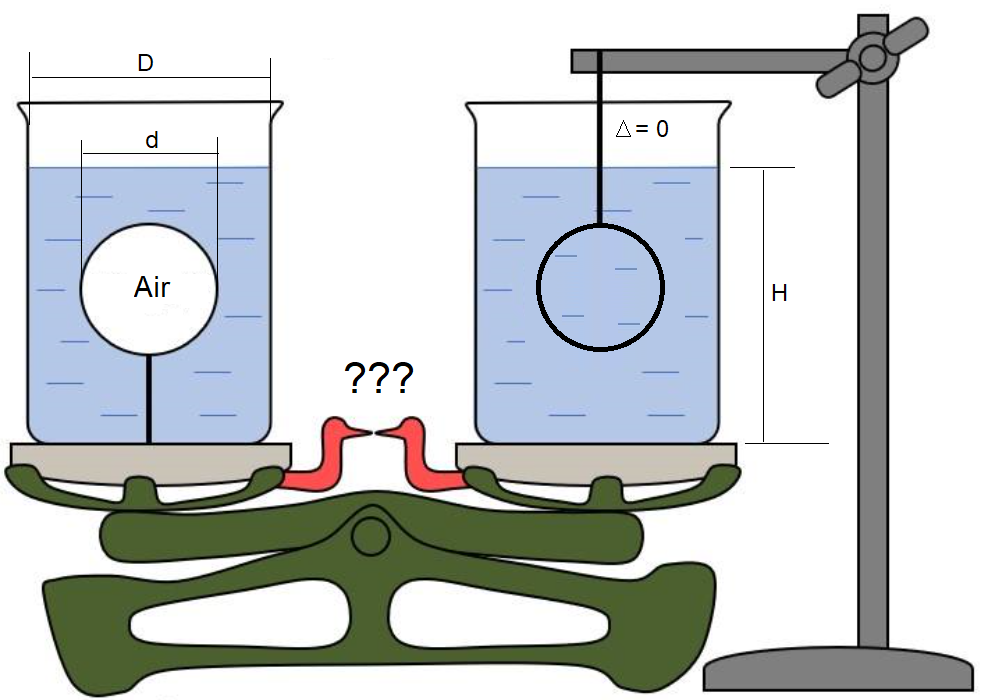
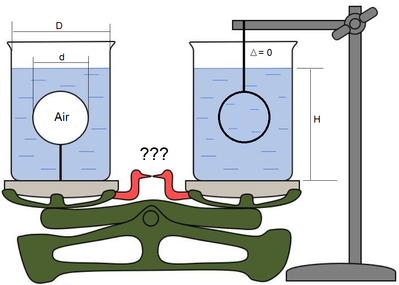
Water, Air, Steel
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
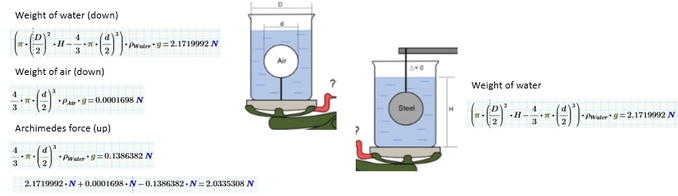
Your calculation of the right scale pan does not account for the presence of the sphere.
Calculate forces!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Turn to right (steel) side.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Valery,
What about the weight of the rope and the balloon (too keep the air in place) on the left side.
Then on the right side, some water is replaced by the rope that keeps the steel ball suspended.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Zero!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Weight of Sphere Air < Weight of Sphere Water
- Tags:
- puzzle
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
>Weight of Sphere Air < Weight of Sphere Water
We have not steel at the right but wood, air or... water.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I don't think I agree with your numerical evaluation Val (though I agree the left side is heavier).
The amount of water is identical on both sides, the weights of the beakers are the same (presumably), the steel ball is externally supported, so the only extra weight on the left side is that of the air in the balloon. The net difference in weight is therefore (4/3)*pi*(d/2)^3*rho*g, which is much smaller than that which you've calculated.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Beaker get the buoyancy force of box and heavier than without box.
- Tags:
- puzzles
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I agree with Alan, yourv calculation for the left is not correct.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry, Fred.
We are not talking about the masses of what lies on the scales, but about the forces that act on the scales. Which way the scales will swing - clockwise or counterclockwise.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry!
One last step:
So the scale swings counterclockwise (left side down.)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I stand corrected!
On the right, the sphere is supported externally; the only addition to the scale is the water in the beaker; it doesn't matter what's in the sphere--the external support reacts all forces.. On the left the buoyancy force on the sphere (Archimedes' force) acts to lighten the beaker.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Your post at 08-07-2020 03:53 PM is right.
- Tags:
- puzzle
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Your calculation of the right scale pan does not account for the presence of the sphere.
Calculate forces!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
My answer of right side include the weight of Sphere Water.
If we remove the Sphere from the water in beaker, the height of water decreases dH.
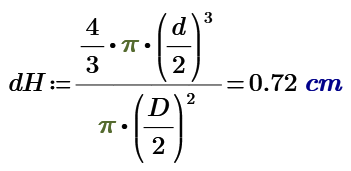
The buoyancy force of air of both side is ignored.
If your answer at 08-10-2020 10:09 PM is right, we can make UFO just using bigger volume sphere than the water volume in beaker.
- Tags:
- puzzles
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This is the answer.
If 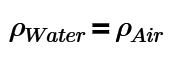
- Tags:
- puzzles
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The net weight of 2000000 ton tanker can fly only using 1L of water without using any energy!
Only change the sphere air volume to 200000 m^3 that is surrounded by 1 L of water.
- Tags:
- puzzle
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
1) You need to study up on Archimedes principle.
2) You should follow Val's work (below.)
3) If you're going to pirate my sheets, please change the names!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you advising me follows.
1) You need to study up on Archimedes principle.
I study it at elementary school or kindergarten.
You also study it again more carefully with Newtonian mechanics.
2) You should follow Val's work (below.)
ValeryOchkov well understand his puzzle. He choice your answer as the solution.
I think if someone feel question to the answer, the one should study his 2^5 text book to understand the problem. If can’t find any error from your answer, the one should also study his 2^5 text book.
3) If you're going to pirate my sheets, please change the names!
Sorry I just use your Mathcad sheet only change the volume of water << volume of air sphere. The answer of your Mathcad sheet is right. In your attached Mathcad sheet, no need to increase the Volume of water. 1 L is enough.
The total weight of 2000000 ton of Oil and net weight of tanker is flying by your buoyancy force equations only using 1 L of water.
May be Werner_E finish our fun discussion?
This is a good puzzle and also good promotion for ValeryOchkov’s 2^5 text book.
- Tags:
- puzzle
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Just to make sure I understood the problem:
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
That's what I originally thought too!
Then I started doing "free body" analysis. The mass calculations you've done are correct. But the buoyancy force on the balloon creates a tension in its string--otherwise it would float to the top, and that tension needs to be reflected in the scales. I think the left rises, the right drops.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
That tension in the rope pulls the bottom of the beaker up. I can understand that reasoning. On the other side of the rope is the balloon, filled with air, it puls at the rope with the same force. But why can it pull, because it sets itself off against the water, which is also in the beaker, and presses the bottom of the beaker down: by its own weight and the same extra force due to the mass of the air in the balloon.
Suppose the water (instantly) freezes; that action should not change the mass of whatever is in the beaker, so the total mass of water and the air inside it remains the same. And if that mass remains the same, so does its weight at that same position with respect to Earth(s gravity).
{One might argue that the beaker breaks due to expansion (Ice has a lower mass by volume than water). My counter argument would be that we'd use a fluid in both beakers that does not change its specific mass going from fluid to solid.}
Since the rope is assumed to have no mass, its length doesn't matter.
Now I try to imagine what happens if the rope between balloon and bottom gets longer. While the balloon is 'piercing' through the water level, the force on/in the rope lowers, but so does the counter force on the water. And finally the balloon hangs just above the water level. No more buoyance, just the mass of the (contents of) the balloon, on top of (mass of) the water is all that makes up the weight on the left side of the balance. But since the balloon itself and the rope have no mass, it's just air on top of the water. There's no distinction with the air that was already there.
That would be different from when the balloon wwould be filled with, say Helium. Helium floats (up) in air. In that case the balloon filled with helium would still be pulling at the bottom of the beaker, bringing the weight down.
Thus I come to the conclusion that my calculation is wrong. The air in the balloon does not count (as does the steel ball on the other side), because air does not float up in air. So the balance in the given example, under the given assumptions, is perfect. Simple.
I wonder where this reasoning goes wrong...
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Right side beaker is also affected by buoyancy force of the sphere volume of water.
It increases the weight of right beaker. The counter force of buoyancy force of the sphere volume of water decreases the weight of steel ball that is suspended by the stand that is outside of beaker. We call this force as Buoyancy force.
- Tags:
- puzzle