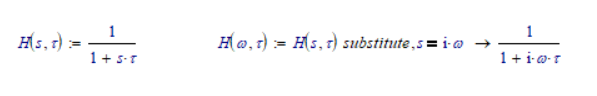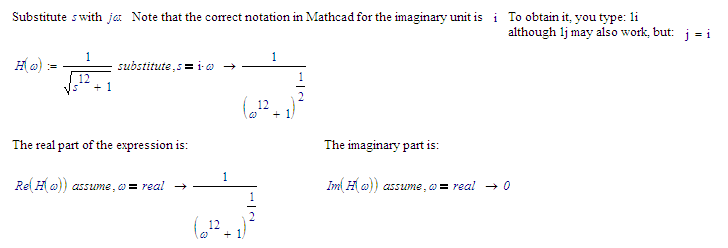Community Tip - You can subscribe to a forum, label or individual post and receive email notifications when someone posts a new topic or reply. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
invlaplace in Mathcad 15
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
invlaplace in Mathcad 15
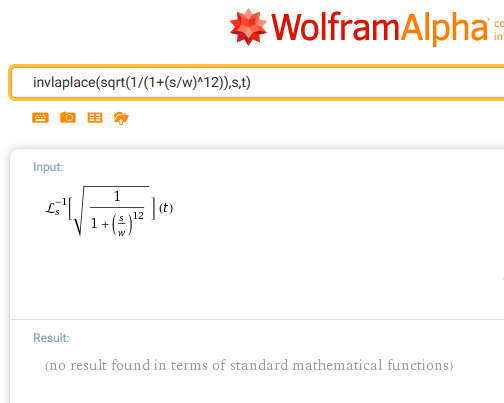
See the attached file. When I try invlaplace in Mathcad 15 with a simple s-function, it works, but with a slightly more complex function, it doesn't give a useful result:
I am a very infrequent user of Mathcad, so please bear with me if I ask stupid questions.
I do not understand the repeated 'invlaplace' and the 's,t' part of the result. I expected a function of t that I could plot after including the numerical value of omega. Setting t=35 and [omega] = 2*pi*t doesn't help.
I tried putting ', omega' after the first 'invlaplace', but it produces no more useful result.
Solved! Go to Solution.
- Labels:
-
Electrical_Engineering
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
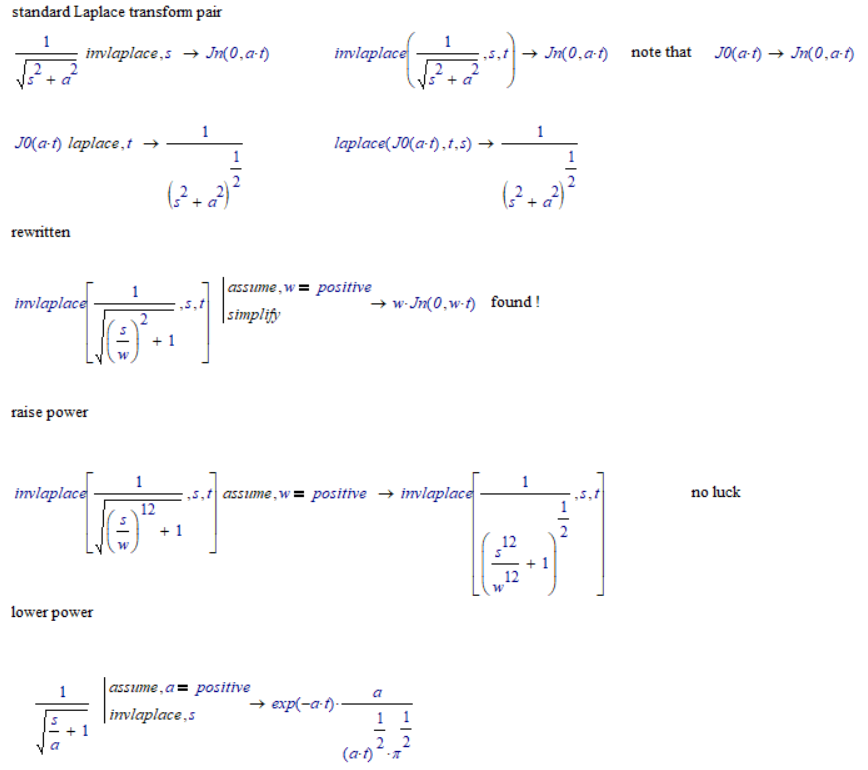
Í don't wish to spoil the fun, but the expression is its own magnitude:
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The result means that Prime is not able to find a symbolic solution for the transform.
The "invlaplace(...)" you see at the RHS is just a function which normally is use internally by the symbolics to derive the inverse laplace.
Writing "omega" after "invlaplace" is definitely wrong as thsi would be interpreted as that the variable in the transform domain, the complex freqency, is named omega in your function.
Default is that the complex frequence is "s" and the variable in the time domain is "t". If this is the case you don't need to provide any further modifyers to "invlaplace" but you sure can write "invlaplace,s,t".
BTW, Wolram Alpha gives up on your function, too:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
desperate 'try anything', because omega is actually a constant, 54*pi in
the case under study.//I am quite surprised that the transform doesn't
work, because the expression is more or less a 'standard form' - the
frequency response of a sixth-order maximally-flat low-pass filter. I
deliberately chose that as 'learning example' because i know the
answer. I wanted to go on to more complex expressions for which I do not
know the answer. Maybe I will try them to see if they can be resolved.
That Wolfram gives up, too, is even more surprising.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The 'more or less standard' would be 1/sqrt(a^2+s^2), the inverse Laplace transform of which is J0(a*t).
Mathcad (that is, version 11, using Maple as symbolic engine) transfoms this pair back and forth.
As shown, you could rewrite the Laplace transfomed as 1/sqrt(1+(s/w)^2), provided that w is positive, but that's still power 2, far from power 12.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mathcad. Matlab handles it, but I don't have it. I'm trying to
understand Octave now, but it's written (even the manual) for code
writers, not Windows users.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Your reaction suggests to me that you have an incorrect understanding of what Mathcad, and Matlab, can deliver.
I'm convinced that neither Mathcad, nor Matlab will give you the inverse Laplace tranform of the expression in s that you gave, based on the fact that Mathematica cannot give it and I didn't find it in my textbooks.
On the other hand I know that both Mathcad and Matlab have functions that allow you to calculate the response in time on a signal through a filter that is described by your expression in s.
In Mathcad look up the butter(), cheby1(), cheby2(), and bessel() functions in combination with iirlow(), iirhigh(), iirpass() and iirstop(). Matlab has similar functions.
You may know that a certain expression in s can describe a specific filter. But you should not expect Mathcad, when requested to deliver the inverse laplace transform of a mathematical expression in s, to react: "hey, this is the expression for such and so filter, so let's give that.". Mathcad, and the symbolic processor of Matlab too, deal with mathematics, and mathematics only.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You are quite right. Invlaplace is not the right approach at all. What I want to do is to take an expression with s as the single variable and substitute omega*i and then rationalize the result (i.e. convert the expression to an equivalent in real quantities) so that I can plot it. I think I have worked out teh syntax for using substitute, but I can't find anything about rationalization in the Help. Perhaps it's called something else
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
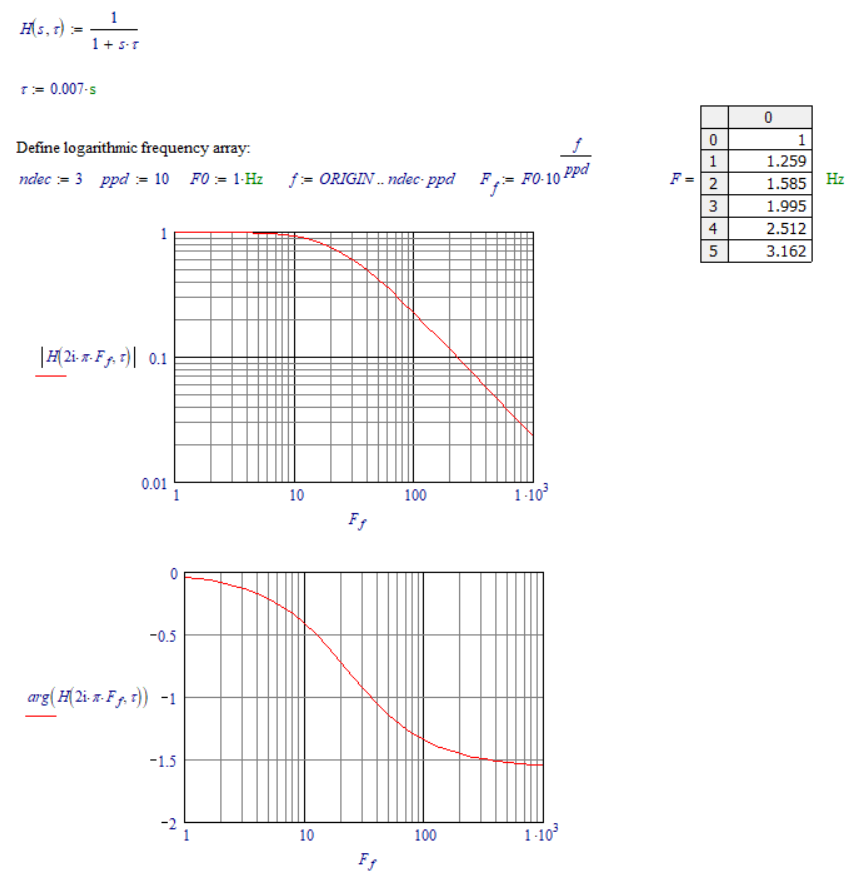
Maybe you are looking for this:
Note that mathcad 15 supports logspace() or so to define a log array.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
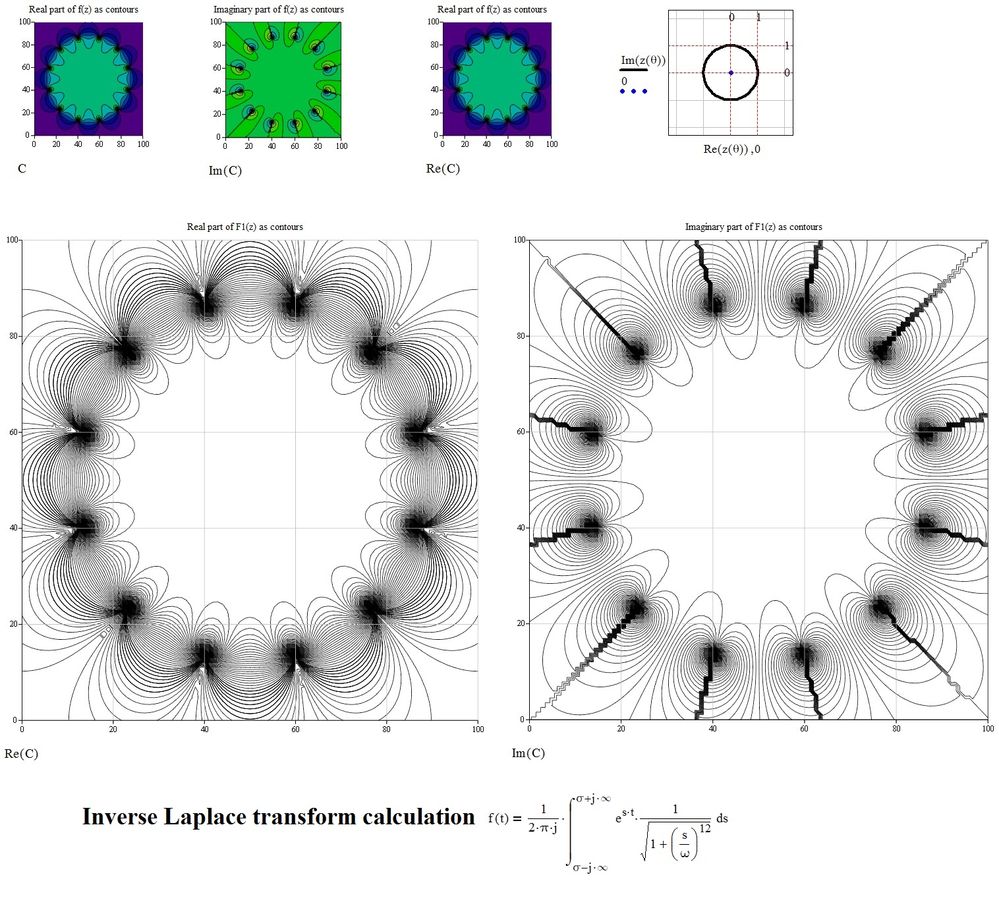
Graph on the Gauss plane of the function of s of which you want the inverse Laplace transform (ω=1.5):
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
don't want an inverse Laplace transform. I need to replace s in the
expressions by omega*i and then rationalize, but I can't find anything
about rationalization in the Help.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
To substitute s with omega*i is simple:
Please explain 'rationalization'...
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
In this file of mine (in fact there would be another four or five) you can find many calculations with Laplace transforms:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
laplace. I just want to substitute w*i (AKA j-omega) for s in a fraction
formed of binomials in s and then calculate the magnitude. I was
originally confused by the way another software uses 'Laplace' as a keyword.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It could be the answer, but 's' should be 's/omega_c', where omega_c is a constant. The imaginary component should not be zero for all omega. I need to check with other expressions in s that seem to give wrong results with other software.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I assume your omega_c is a (real) constant. Dividing s by it does not make a big change, and it certainly will not help in getting an imaginary part for the total expression. Note that you raise s (or s/omega_c) to the 12th power. Since that power is an even number, and with s replaced with j*omega, you're effectively raising j to the 12th power. That will make it real.
If, however, you keep s as a complex number (with a complex and a real part, both non-zero) you will get a real and a complex part for the total expression.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
for the magnitude is /sqrt(1/(1+X//^12 //))/, where /X/
=/omega//omega_c, omega_c being a constant. Of course, being a
magnitude, this is a real quantity. In this sort of expression for the
frequency response of an electrical filter, the exponent is always even,
being twice the 'order' of the filter, a whole number.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Í don't wish to spoil the fun, but the expression is its own magnitude:
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
close this thread now. Since the title is very misleading, the moderator
should consider deleting the thread.
With thanks to all who offered help.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I'm afraid that's not how it works.
I suggest you mark your last reaction as the answer to this topic, in that case it will be moved to the top, and people who are looking for info can still read what was going on.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
thread adds nothing useful for explaining the invlaplace keyword.