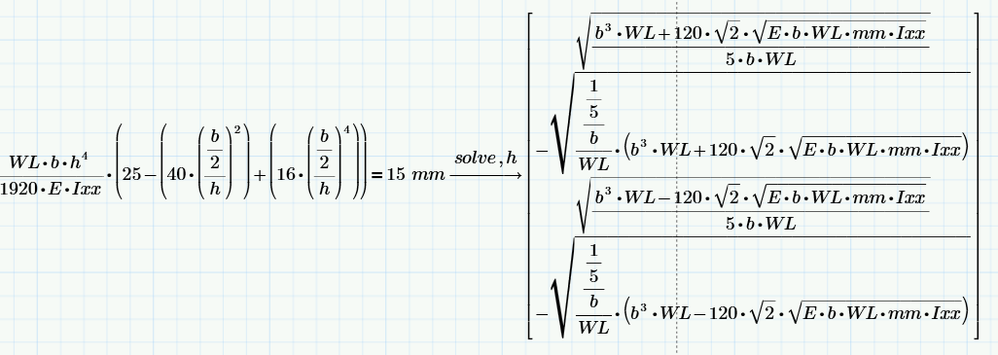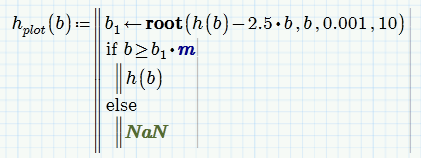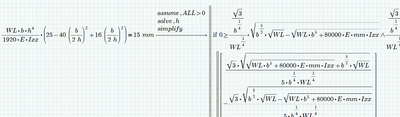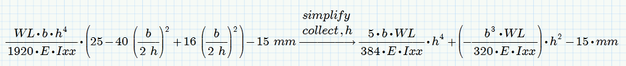Community Tip - Need to share some code when posting a question or reply? Make sure to use the "Insert code sample" menu option. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
operator - solve
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
operator - solve
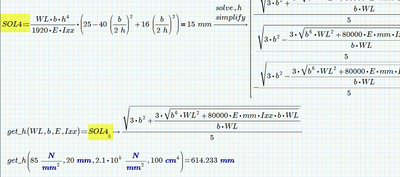
Hi
Please help me to find the h value using operator and solve h. I got 4 answers . How can I select the absolute value from the answers.
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
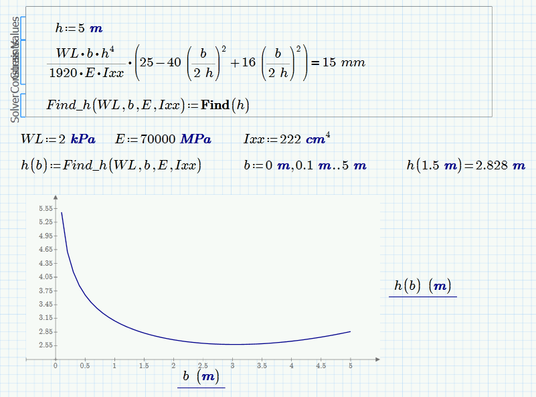
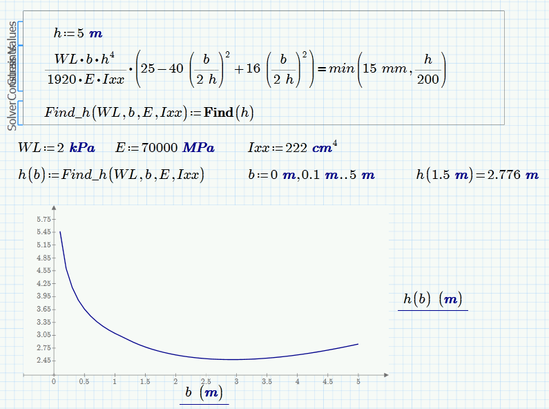
What I see in the pictures is that in the first case (=15 mm) is that for values of b greater than 2,2 m the solve block returns the negative solution from time to time. The solution returned depends on the guess value. fortunately in your case its easy - simply chose a greater value as guess. I have chosen 5m and all seems to work OK.
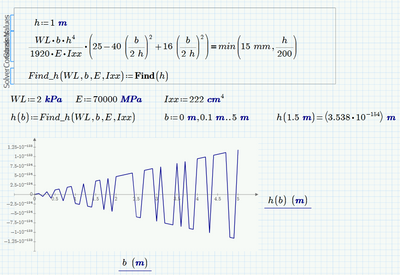
For the second case I can't duplicate your result
Fortunately simply enlarging the guess value seems to cure it here, too:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ldante wrote:
Hi
Please help me to find the h value using operator and solve h. I got 4 answers . How can I select the absolute value from the answers.
Four solutions seem OK for me for that equation. How many solutions did you expect?
And what do you mean by "select absolute value from the answers"?
Do you mean how to select the postive of the four (if there is any or only one).
Answer: You cant, as we don't know anything about the other variables WL, b, E, Ixx, mm in use. They could be positive, negative, non-real and all that would change the output. Also the relatives magnitudes of the variables matter. So Prime can't decide, which of the four solutions is postive or even real.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
One solution only is fine
Can I have a solution also if this is the case ?

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ldante wrote:
One solution only is fine
But a polynomial equation of fourth order has four solutions - thats math. Xou can't change that 😉
Can I have a solution also if this is the case ?
Guess, no.
Maybe in a solve block when all other variables are given, too.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Addendum
If you are happy with just the first top solution the sombolics gives you, you may turn it into a function that way:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is the solve block I was talking about. I turned it into a function of the unknow variables for universal usability
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
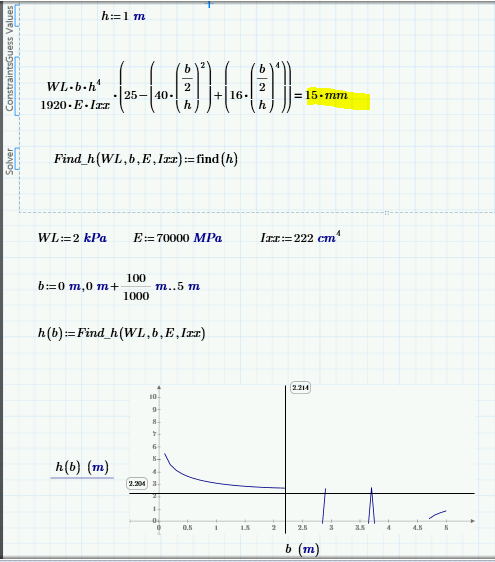
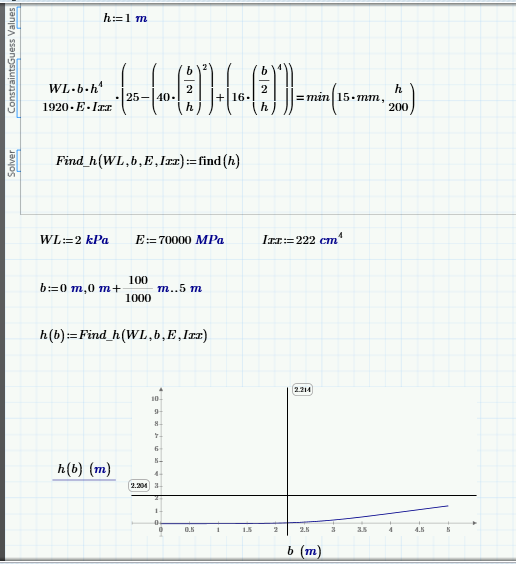
Hi Werner,
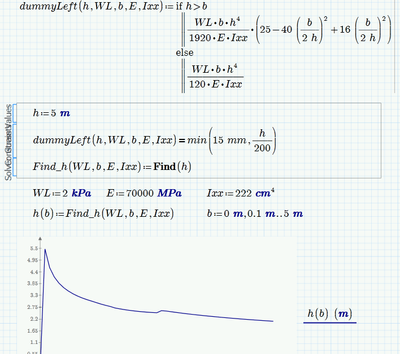
Thank you this maybe working and close to the result I needed. If you can see from the image I attached ,when I used 15mm the graph seem to be right , but if I consider the condition of min(15mm,h/200) the graph is different and not close to the result . Do you think solve block will work if I used IIprogram if II?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
What I see in the pictures is that in the first case (=15 mm) is that for values of b greater than 2,2 m the solve block returns the negative solution from time to time. The solution returned depends on the guess value. fortunately in your case its easy - simply chose a greater value as guess. I have chosen 5m and all seems to work OK.
For the second case I can't duplicate your result
Fortunately simply enlarging the guess value seems to cure it here, too:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Werner,
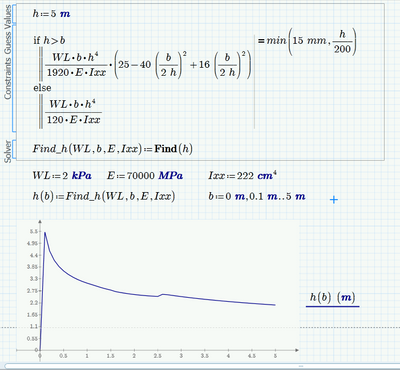
You save my day. thank you very much. I have another condition where the formula will change to triangular. how we will do this in the solve block.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry the triangular formula should be like this
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I have another condition where the formula will change to triangular. how we will do this in the solve block.
The h^3 in the else branch seems to be a typo (you will get a unit mismatch). Should be h^4 as in the first case I guess.
You may do it that way
but I would prefer for better readability to turn the LHS into a function (you sure will find a better name for it)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
cool ![]()
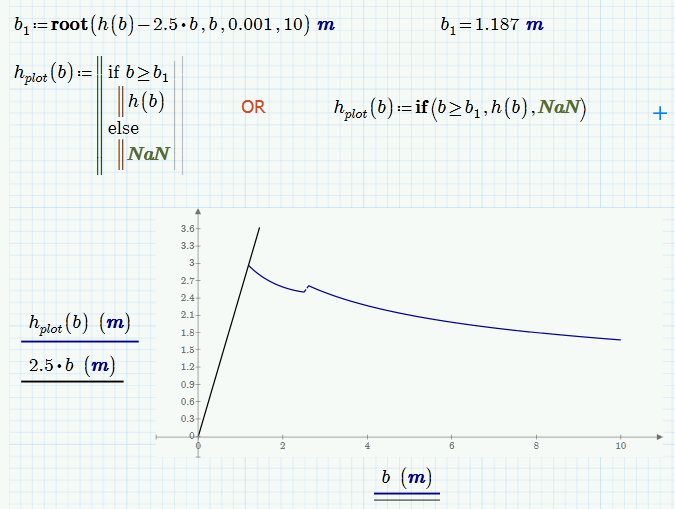
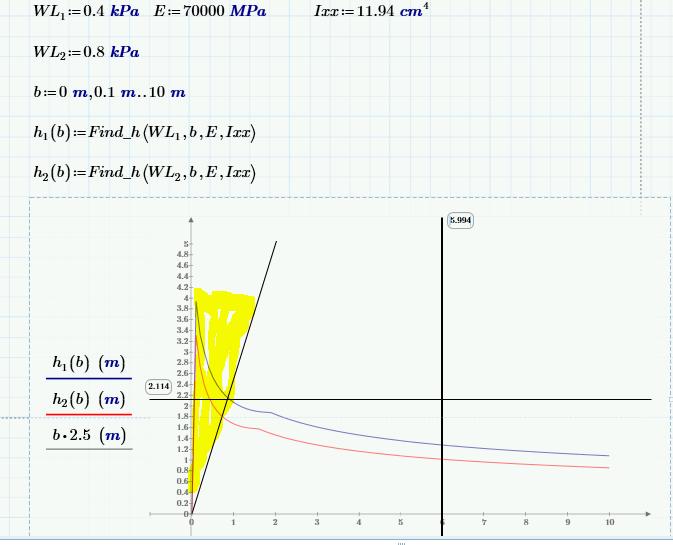
Another one . how I will remove the line in the shaded part of the graph ? if I will use b=0,0.5,..10 the curve become straight line.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thats tricky.
First you would have to determine where h1(b) and the straight line cross (using "root" or a solve block). Lets call the position found b1.
Then you would create a new function for plotting, like
h1_plot(b):= if b>=b1 then h1(b) else NaN
NaN (not a number) will not show up in the plot.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
help ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ldante wrote:
help
????
You maybe tempted to use
but this is inefficient as b1 is calculated with root for every point plotted
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
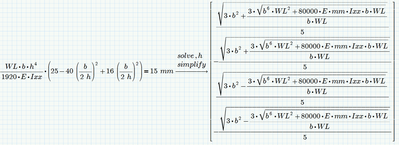
You could simplify the expression
and so you can see, that if all variables are positive, the first solution will be positive, too, the second will be negative.
We can't say anything about the third solution in that case. If its real it will be positive, too, but we can't tell without knowing the values of the other variables.
You can tell Mathcad that alll variables including the searched for should be positive, but I guess you don't like the result:
If you simplify the equation you want to solve you see, thats it a simple biquadratic equation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Idante,
To get absolute values you must define all variables for instance E:=2.1*10^5N/mm², etc.
Then we have four solutions which must be discussed according to clarify what result is practicable and realistic.
What you found is a complete symbolic solution with four results for an equation of 4th degree.

Hope the attachement helps.