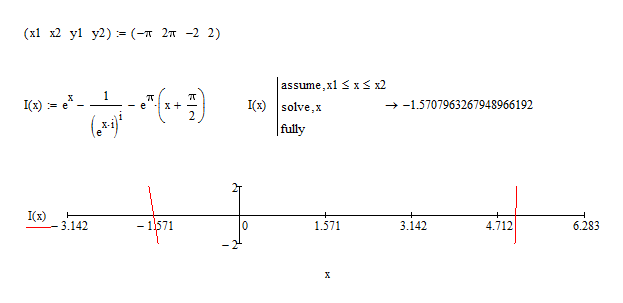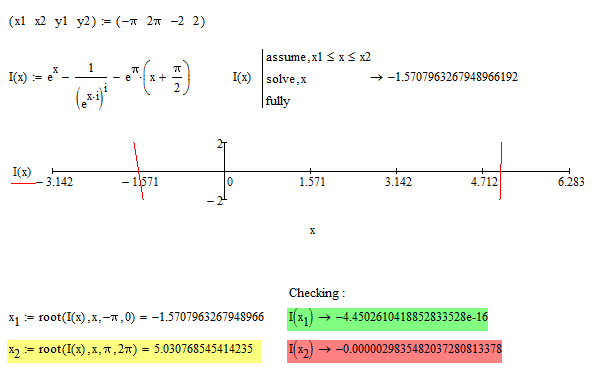
solve , x , fully ?

[lvl107]

  Hello Everyone.

From :

solve , x , fully ?
     Thanks in advance.

            Regards.

[LucMeekes · Accepted solution]

You have found all zero's. Here's what's going on:

Success!
Luc

[lvl107]

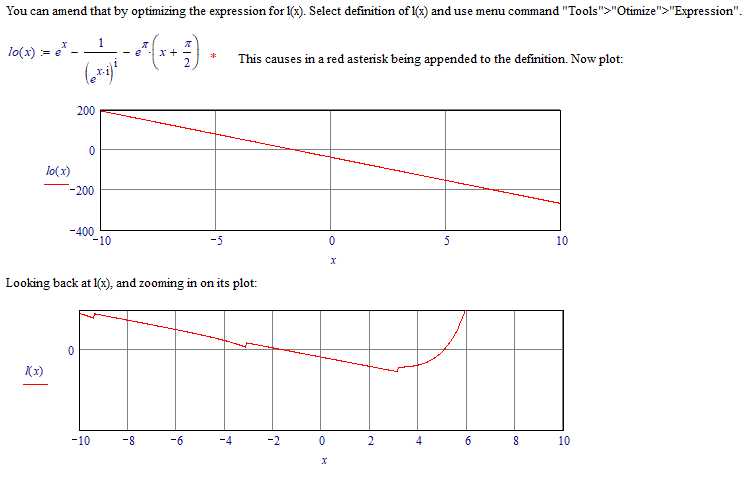
I appreciate your time and help, Luc.  ( It seems MC15 does not show  optimize>>equation. ).The query : "Is there a any way to make more precision for the "yellow".

Best Regards.

[Werner_E]

Mahcad 15 knows "optimize": Right click the expression an from the pop up menu chose "Optimize".

You get better precision with numeric calculations if you decrease the value of the system variable "TOL".

Set it to something like 10^-10. Either from the menu in "Tools"-"Worksheet Options"-"Built-In Variables" or just type TOL:=10^-10 at the top of the sheet (or use a global assignment).

[LucMeekes]

Be aware that you are chasing a ghost. As I demonstrated that that root does not exist for the equation that you give. It's a numerical anomaly.

Success!
Luc

[lvl107]

I guess that I need the explaining.

Best Regards.

[lvl107]

and how differrent ?

Best Regards.

[Werner_E]

---

@LucMeekes wrote:

Be aware that you are chasing a ghost. As I demonstrated that that root does not exist for the equation that you give. It's a numerical anomaly.

---

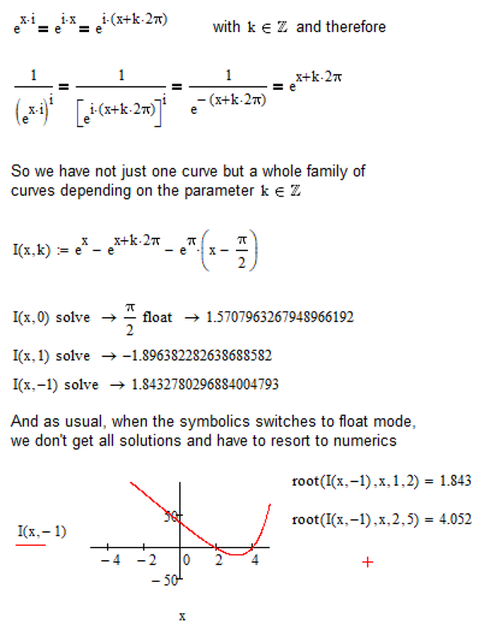
No, its not. And there even are further roots. The point is the expression e^(i*x) or (e^(i*x))^i which Maple believes to be just e^(-x).

But here muPad knows better (its standard domain is complex, not real) and so it does not "simplify" that expression the way Maple does. One always has to be aware which rules know from real numbers still apply when we deal with complex numbers. In complex numbers we often are confronted with some sort of ambiguity.  Keep in mind that

The problem with the numeric evaluation of the original function is that it will jump from one member of the family of curves to the next which you interpreted as numerical anomaly.