Community Tip - You can subscribe to a forum, label or individual post and receive email notifications when someone posts a new topic or reply. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Pendulum Math model
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Pendulum Math model
Why someone is not correct?
See lpease the picture and Prime 3 sheet in attach.
- Labels:
-
Calculus_Derivatives
-
Physics
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
First of all--it's Prime 6, not 3. (Since I'm using 4.0 Express, I could tell.)
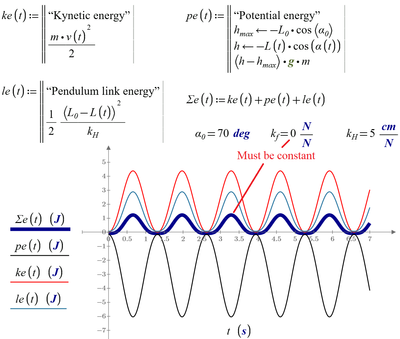
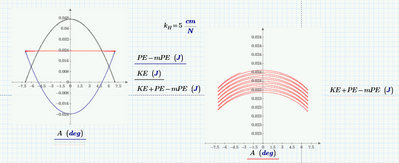
Second--Potential energy can't be negative (I understand why you're showing it that way, but . . .)
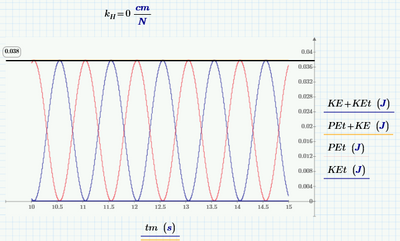
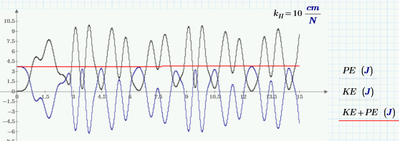
In the absence of dissipation, and if the pendulum is rigid, total energy will be constant. So if we make kH = 0, we should get a graph like this:
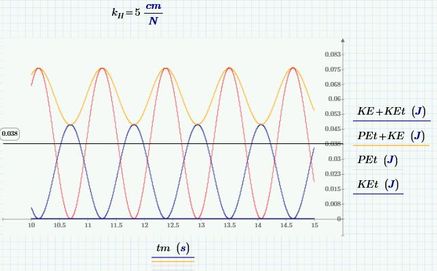
I have put a marker here on the total energy level. Now, if we let the pendulum be a spring:
The calculated potential energy is WAY TOO HIGH. The kinetic has increased too, but there's only so much energy to start, and both calculations started at the same condition.
Attached is the (somewhat messy) Prime 4.0 Express sheet.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry, a potential eneggy can be negativ - see please the picture (a hard link!).
May be the problem in the function for le.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You're right, of course; the potential energy is defined relative to an arbitrary zero point.
There are two potential energies to be tracked:
And two kinetic energies:
And, if I did it right (within calculation accuracies) they now track:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry but v of vibration is one part or common v.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I don't understand your comment.
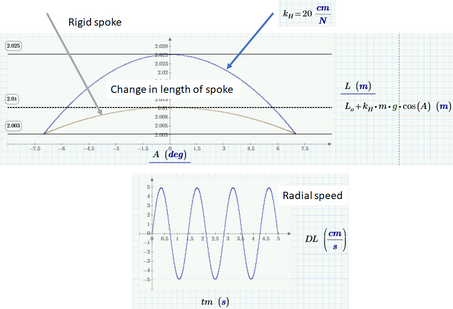
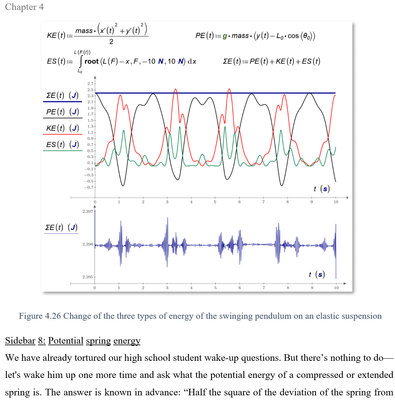
This represents two coupled harmonic oscillators: a pendulum, and a spring/mass. Each trades potential energy and kinetic energy back and forth, so we need four energy calculations. If we're not careful in our definition of reference potential energy (I chose the bottom of the pendulum swing, but that changes as the spring constant of the length changes) then the calculation will not be valid. Take the pivot point of the pendulum as the zero potential energy point for the pendulum; all potential energy for the pendulum will be negative as long as the angle stays below 90°. I also chose the un stretched pendulum length for the zero reference for the spring/mass.
Latest effort attached. Feel free to play!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry, Fred!
We have a physical point (mass without size) and a weightless non-bendable spoke that compresses or stretches according to Hooke's law.
There are three energies:
- kinetic energy of a physical point
- potential energy of a physical point
- energy of compression or stretching of the spoke
The sum of these three energies must be constant if we do not take into account friction (k_f = 0), or it must decrease (k_f > 0).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
We have a physical point (mass without size) and a weightless non-bendable spoke that compresses or stretches according to Hooke's law.
There are three energies:
- kinetic energy of a physical point
- potential energy of a physical point
- energy of compression or stretching of the spoke
The sum of these three energies must be constant if we do not take into account friction (k_f = 0), or it must decrease (k_f > 0).
a weightless non-bendable spoke that compresses or stretches according to Hooke's law. This is a spring! And the "physical point" is moving radially as the non-bendable spoke compresses or stretches. So there is a fourth energy, the kinetic energy of that radial motion.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Fred!
Create please the Prime 3 sheet - see attach.
With 4 energies!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
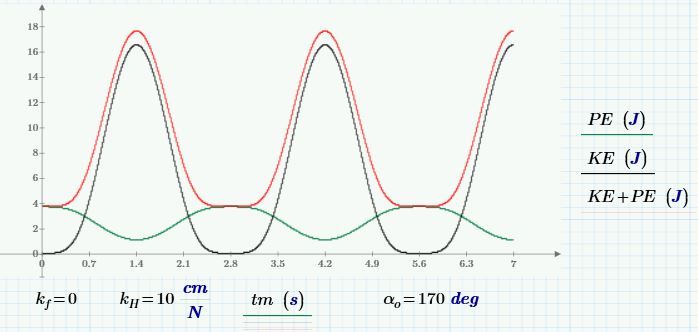
Per your request.
Note:
- The Prime sheet is 4.0 Express. You can copy individual expressions from one version of Prime to another.
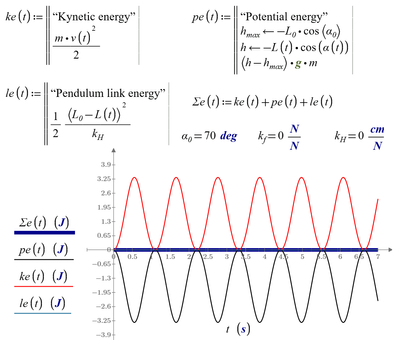
- The expression for pendulum potential energy is incorrect for starting angles above 90°.
- If you freeze the spoke (kH = 0), the energies still sum to zero.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
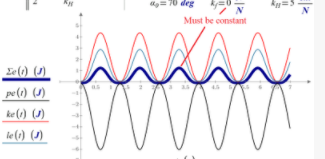
I would like see the plot - the summ energies as function od time at k_f=0 it is ___________________________
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I would like see the plot - the summ energies as function od time at k_f=0 it is
Can you not execute my sheet? It's easy to change parameters, it's your table!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry, Fred!
Where is the line_________________________ on the second plot?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry Valery,
This was your project:
I'm just trying to help. Both of us are missing something, where is your input? 🙂
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Courtesy of Wikipedia:
Had to drop the friction damping (at least first pass)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OK!
And what about the spring energy?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
And what about the spring energy?
You could define (as I had before) defined pendulum and spring energy separately; but you'd need to take the vector magnitude "sqrt(Vp^2 + Vv^2) to add them together. Please also note that the solver is different from the previous version. Velocities, lengths, and angles report different trajectories. (Haven't figured out why just yet.)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I have solution for a 2D problem with the non-linear Hook law.
But no for 3D one