Community Tip - Did you get an answer that solved your problem? Please mark it as an Accepted Solution so others with the same problem can find the answer easily. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
How to enter differential equation?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How to enter differential equation?
How do I enter this differential equation into Mathcad 15, and make it find the symbolic result?
f'(x)=1+f(x)
solve for f(x)
( where f'(x) is the derivative of f(x) )
I know the answer is
f(x) = e^x - 1
Thanks
Solved! Go to Solution.
- Labels:
-
Calculus_Derivatives
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Jason,
At each differential equation, you have to associate the initial conditions.
The simplest method to solve the given type I first order ordinary differential equation, is the following:
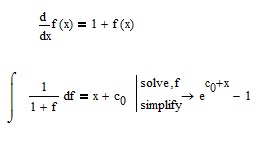
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
LOL yes I did use W.A., but I wanted to know how to enter it into Mathcad ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Jason,
At each differential equation, you have to associate the initial conditions.
The simplest method to solve the given type I first order ordinary differential equation, is the following:
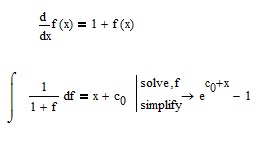
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks all.
I've been a heavy user for many years, but embarrassingly, I've never used the below syntax, and don't know how to type in the circled part:
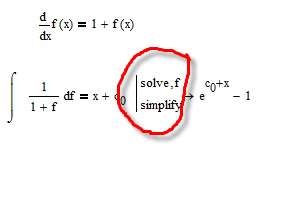
Could someone nudge me in the right direction? What key stroke or mouse click? Which toolbar?
TIA!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Jason

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks!!!
BTW what did you use to create the above tutorial image?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This is achieved with a patient copy and paste work. You must click on the "Print" button of the first row of keys on the keyboard, to copy in memory the current screen, then paste it into Paint (windows). Reduce the image, and clicking outside the image, uncheck the same. Then, select the part that interests you, and cut it. Press the undo button until you get the blank page, then paste what you had selected, and so on.
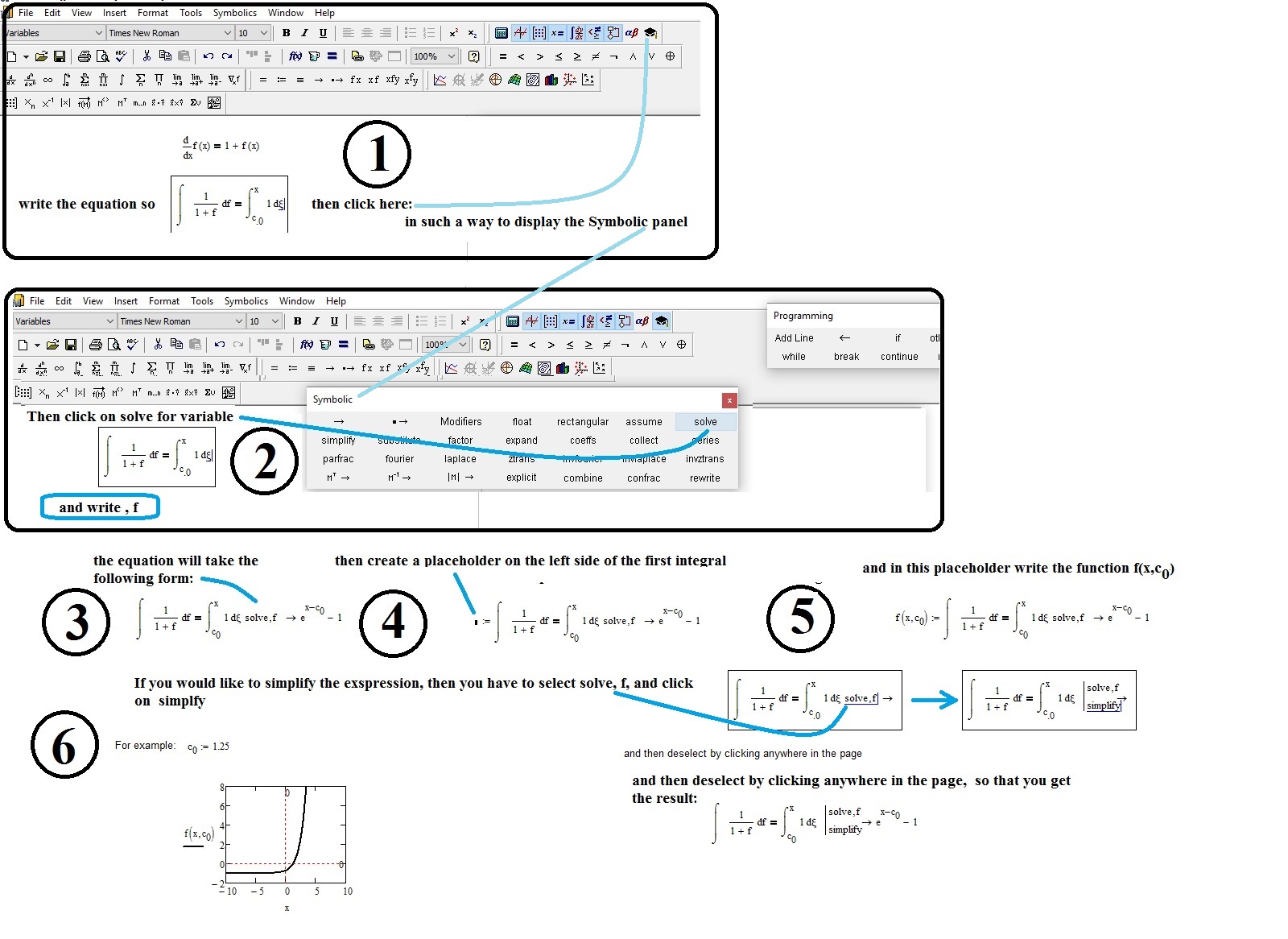
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Note that the solution to the DE you provide is not THE solution but A solution to that DE.
Unfortunately Mathcad, nor Prime, provide a feature to solve for differential equations symbolically.
F.M. shows a nice way of working around that, above.
Then of course there is this method (A classical math problem: differential equations), which can be automated in Mathcad 11, but requires some hand work in later versions.
Wit your specific example:

Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You were already told that Mathcad can't solve differential equations symbolically automatically. You have to do it manually and Mathcad helps you with the integrals.
But for the case of very simple ODEs of first order like yours, long time ago I once wrote a small routine (VdK) to solve them automatically (its for Mathcad 15 (and below)). Maybe you find it useful.
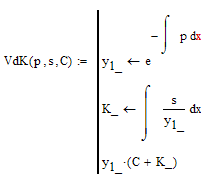
VdK assumes that the independent variable is named x. There is also a routine Vdk2 in the attached file, which can deal with arbitrary variable names. As far as I remember that was the tricky part ,-)






