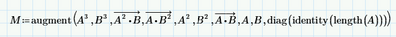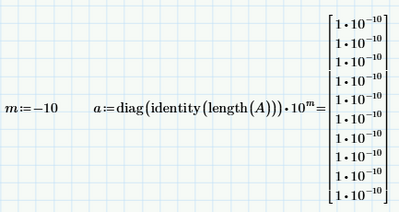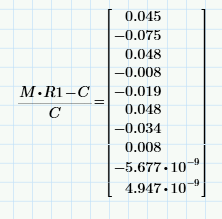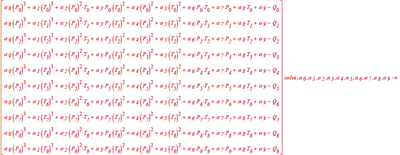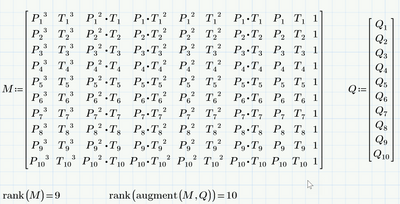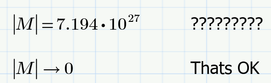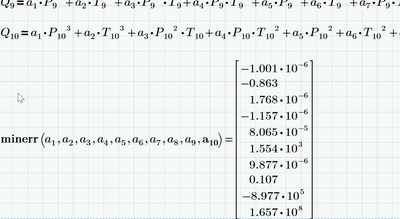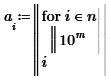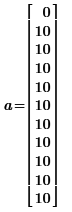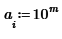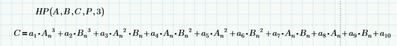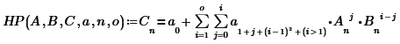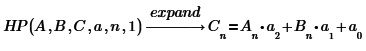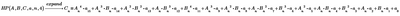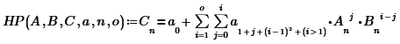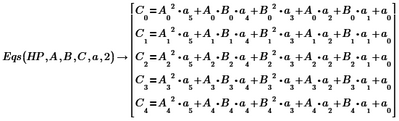Community Tip - Need to share some code when posting a question or reply? Make sure to use the "Insert code sample" menu option. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
No solution found for solveblock
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
No solution found for solveblock
I am getting error no solution found for solve block I tried to change the value for TOL and CTOL but with no luck
Solved! Go to Solution.
- Labels:
-
Mathcad Usage
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I can get minerr to work on (what I think is) your problem:
with:
You can define a matrix M with:
Which means that M is:
The rank of M is still 9, instead of 10, and its determinant is still 0 (according to the symbolic solver), so there is not a single, unique solution; this is still the same problem you had before.
Now you want to solve a in M*a=C, using minerr (that is, find a solution that is close).
Your guess values for vector a can be constructed with:
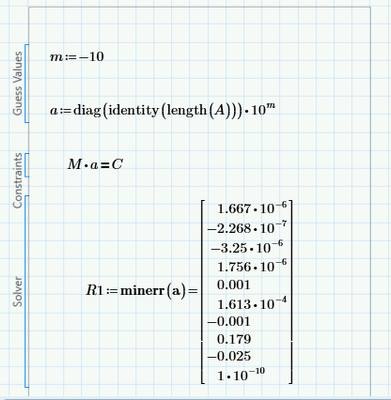
Your solve block might look like this:
And see, it produces an answer. But how good is it?
M multiplied with R1 should produce C. Let's see:
We can calculate the relative errors:
C9 and C10 are pretty closely obtained, but C2 is 7.5 % off.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You have 10 equations, and 10 unknowns, but that does not guarantee there is a solution.
Assuming this set is equivalent to yours:
I get no symbolic solution, which may indicate that the equations may not all be independent from every other.
Are you sure this must lead to a solution?
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
As Luc already suspected there is no solution for your system using the numbers you provided for the P, T and Q variables.
As you can see in the screen shot below, the rank of the coefficient matrix is less than 10 (which means there is no unique solution, either none at all or an infinite number of solutions). Because the rank of the extended c.matrix is 10 this means that the system has no solution.
Changing some input values can make you system solve. As an example if you change T5 from 600 to 601 the system has a solution.
rank(M)=9 should also mean that the determinant of the matrix is zero, but Primes numeric thinks its as large as 10^27! That seems as a severe bug to me. The symbolic evaluation returns the correct result.
Because the numeric thinks that the determinant is not zero, it will also calculate an inverse of M and you could use this to calculate the solutions for the a-values.
But because the determinant actually is zero and the determinant therefore not invertible, you sure should not trust those results 🙂
You may also use "minerr" instead of "find" in your solve block to find a best approximation. Not sure if those values would be of any value for you, though.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you @Werner_E Werner for your inputs due to some conflicts I cannot share the files here in community.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I tried to genialize the worksheet and trying to solve it in a way you mentioned somehow i am still getting error. Can you let me know what i am missing in here?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
For a start...
Your construct:
does not lead to the result you (most probably) had in mind. The result of a program is the value of its last executed statement. In this case that is
i
And since i has a final value of 10, your array a is a 11-element array, where the first element is 0 and all remaining elements have the value 10:
How come 11 elements? Well... Mathcad indexes arrays starting at the element with position 0 (zero), by default. So you get this extra element. The index of the first element is controlled by the built-in variable ORIGIN.
Type
ORIGIN=
somewhere on your sheet and you'll see it gives the value 0.
You can set it to 1, via the menu, or by assigning it that value, like:
ORIGIN:=1
at the top of the sheet.
OK, Let's assume you've put ORIGIN:=1 at the top of your sheet.
Now you must realise that a range (such as how you defined i and n), is in fact a form of iteration. This means you can simply have the array a take on the values 10^m for each of its elements as follows:
This will simply iterate through all values of i (from 1 to 10) and assign the corresponding elements of a the value 10^m.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I changed the origin to 1 but it did not provided me any result. I am trying to iterate the solution within loop can you help me to debug it or show how it can be done in prime?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I can get minerr to work on (what I think is) your problem:
with:
You can define a matrix M with:
Which means that M is:
The rank of M is still 9, instead of 10, and its determinant is still 0 (according to the symbolic solver), so there is not a single, unique solution; this is still the same problem you had before.
Now you want to solve a in M*a=C, using minerr (that is, find a solution that is close).
Your guess values for vector a can be constructed with:
Your solve block might look like this:
And see, it produces an answer. But how good is it?
M multiplied with R1 should produce C. Let's see:
We can calculate the relative errors:
C9 and C10 are pretty closely obtained, but C2 is 7.5 % off.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Is it mandatory to generate the general format of polynomials automatically? You created for M, as the polynomial I am solving is of 3rd degree and would to increase it to 5th
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You can easily extend it to 5th order. But if you want to include all cross products of A and B, your vector a will need to increase in length. And you'll need more equations, requiring longer A, B and C vectors as well.
As for the creation of equations: matrix M is easily enlarged by adding more expressions to the augment() function.
Most important is that you ensure that the data is such that the rank of M equals its number of rows (and columns), by choosing suitable values for A and B elements.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you for the information. I would like to know what function in MathCAD prime could give me the general format of a specific polynomial.
For example, is there a function like
is there a function in MathCAD that can do such a thing?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
No, not built in, you'd have to write your own function. This comes close:
It gives
and
but then:
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You can even use this function to construct the necessary set of equations:
Fed as Eq to:
Gives:
But more elegantly, AND to show that your set of input data is the cause for not finding a solution to your problem is:
The above function creates the coefficient matrix for a ' polynome' of order o, example:
Now create a set of random vectors A, B and C for order 3:
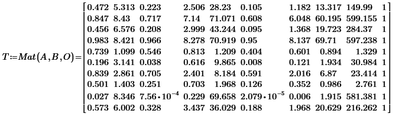
That gives a coefficients matrix:
Which allows to find the vector a that satisfies T*a=C with:
Where
Check:
Note that the values of C are order 100, so the relative error is 10^-13/100=10^-15, that corresponds to 15 digits and to the precision of Prime's numeric processor.
Note also that for this (random) example, the rank of T is:
Success!
Luc