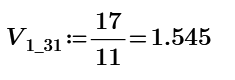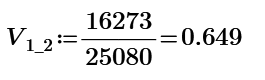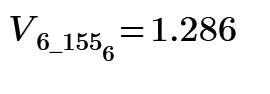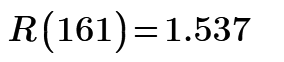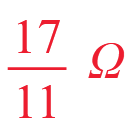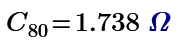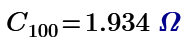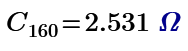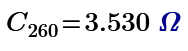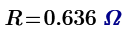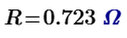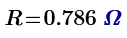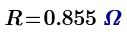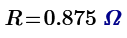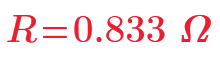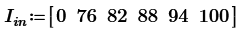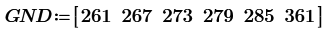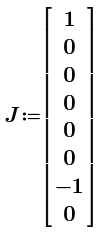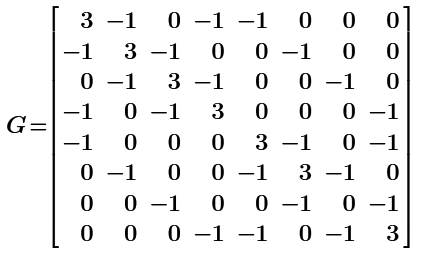Community Tip - Your Friends List is a way to easily have access to the community members that you interact with the most! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
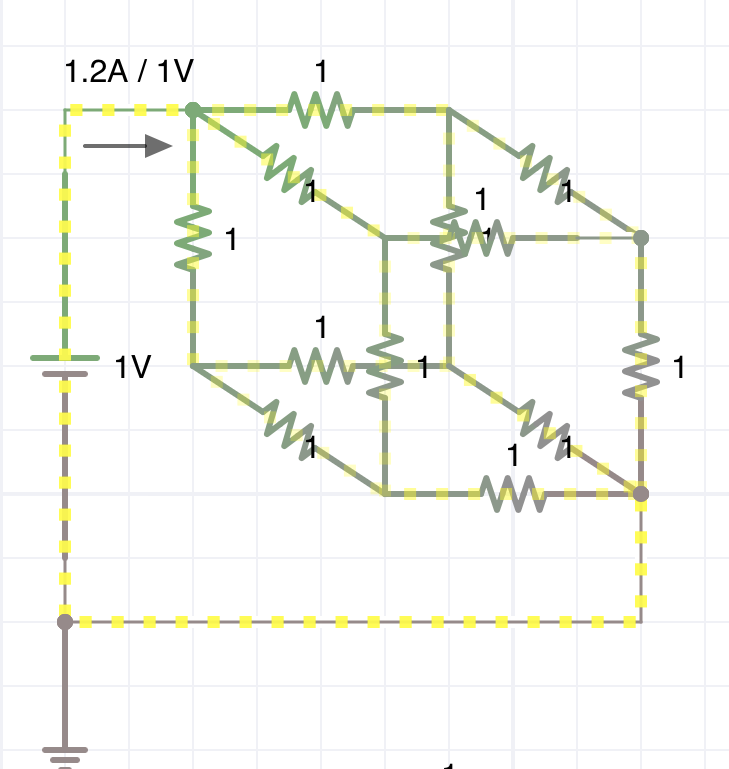
Solve diagonal resistance of resistor 3D mesh.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Solve diagonal resistance of resistor 3D mesh.
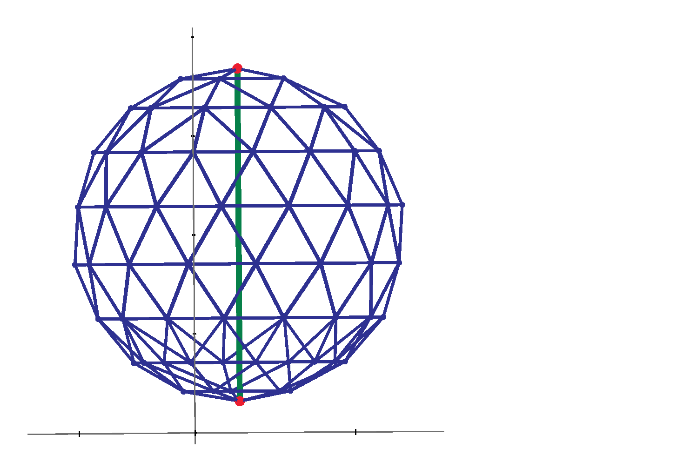
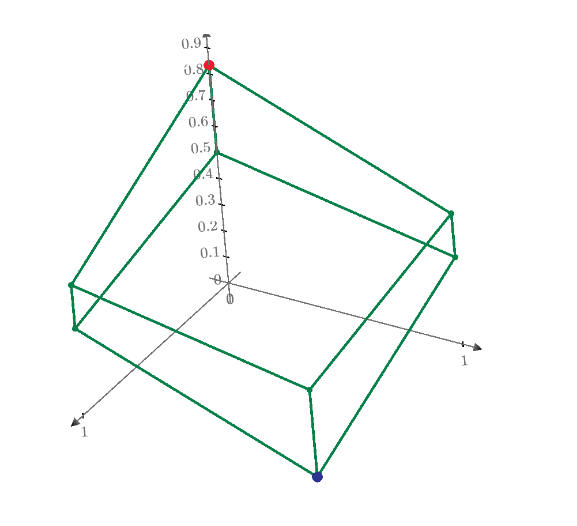
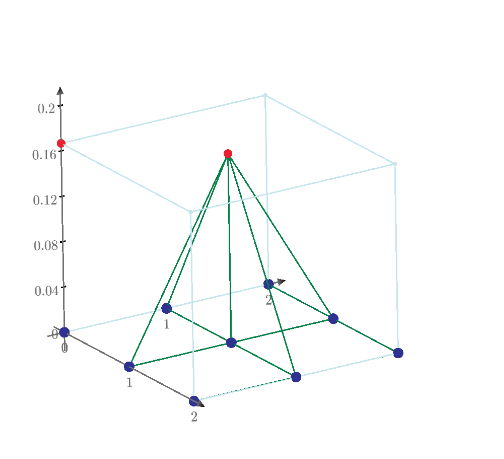
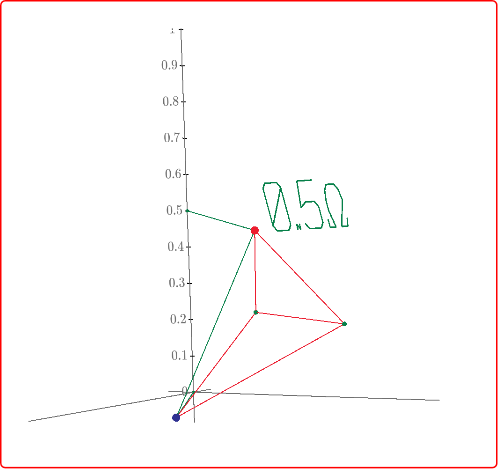
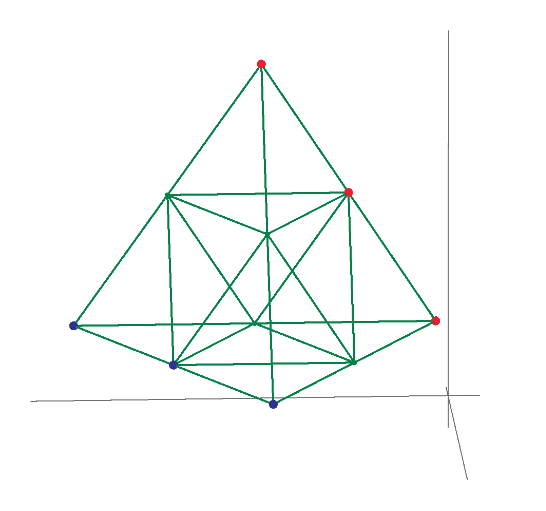
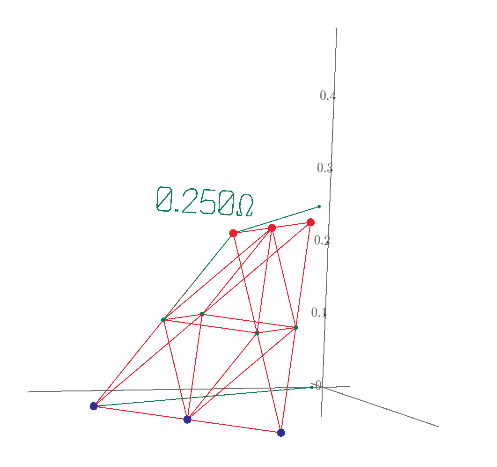
Diagonal resistance of regular polyhedron. R(4)=1/2, R(6)=5/6. How about R(8), R(12) and R(20)?
Solved! Go to Solution.
- Labels:
-
Electrical_Engineering
-
Puzzles Games
- Tags:
- Electric_circuit
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
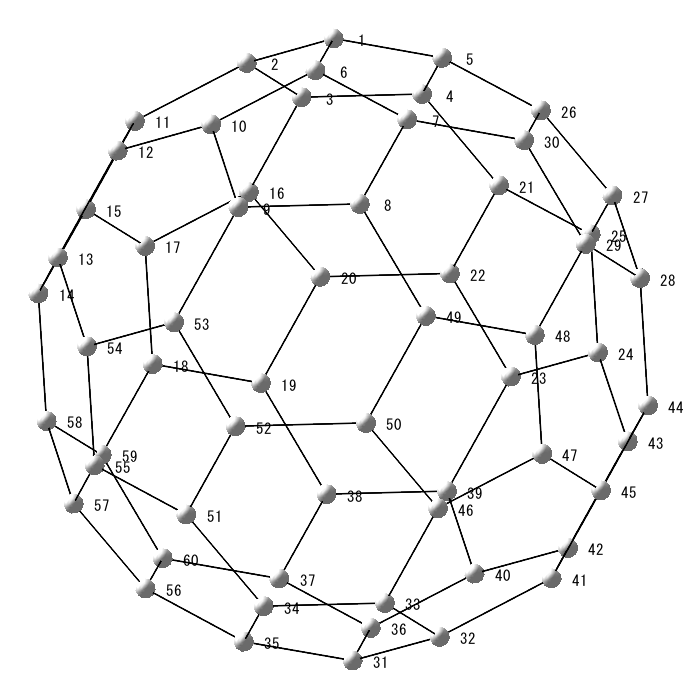
Resistor mesh of 60 nodes is made by Maple 2021. Resistance of node 1 to 31 is 17/11 ohm. The one of node 1 to 2 is 0.649 ohm. Not sure this is true but Mathcad can solve them.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I don't know why every body went to town on this. You already gave the V and I so R = 5/6 ohms.
But as an academic exercise - as others have given but more colourful pictures are here:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
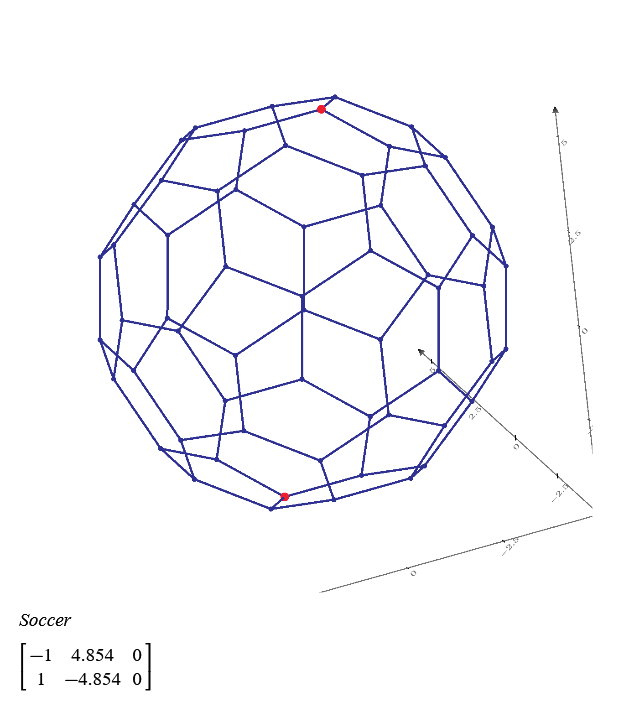
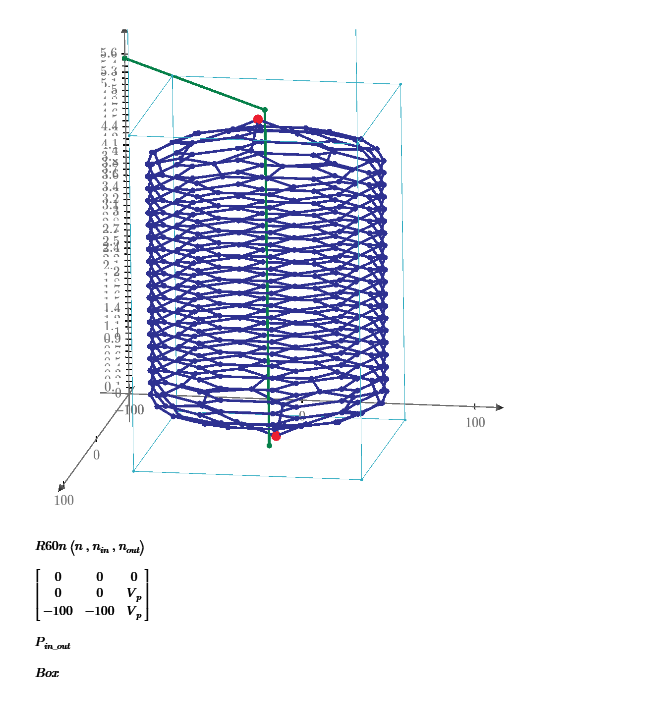
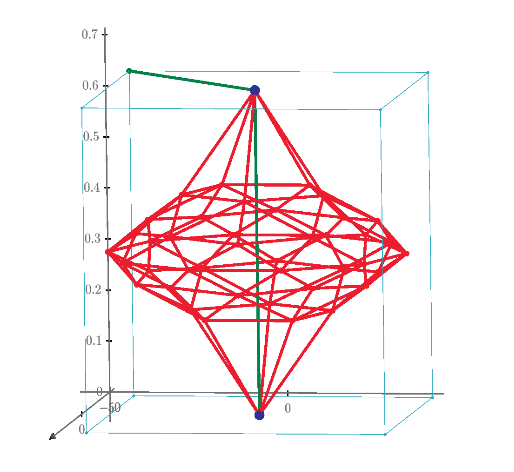
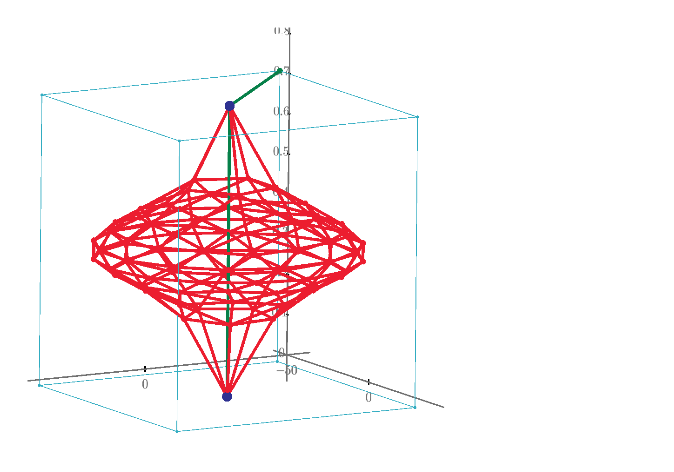
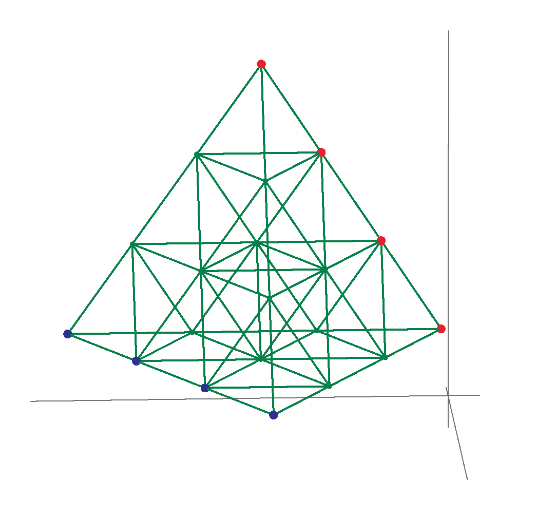
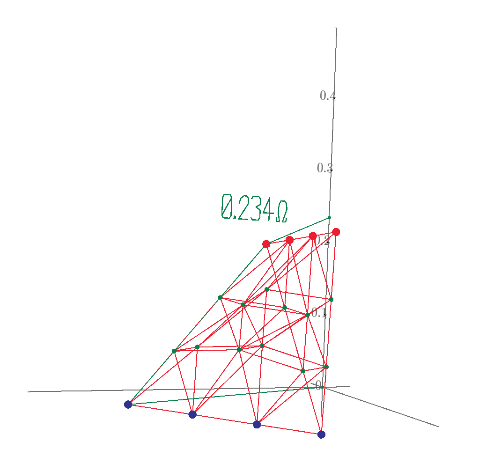
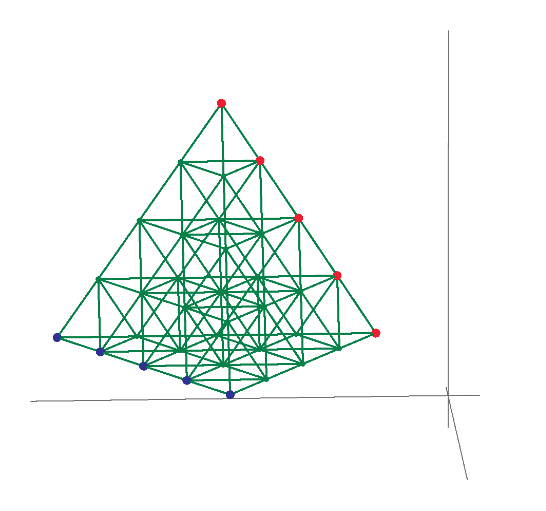
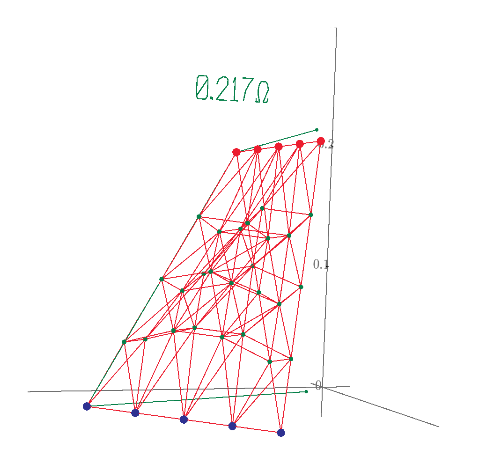
This is not solving 3D 1*1*1 grid resistor mesh only. Using Mathcad or other mathematical programs we can calculate more interesting resistor grid problems.
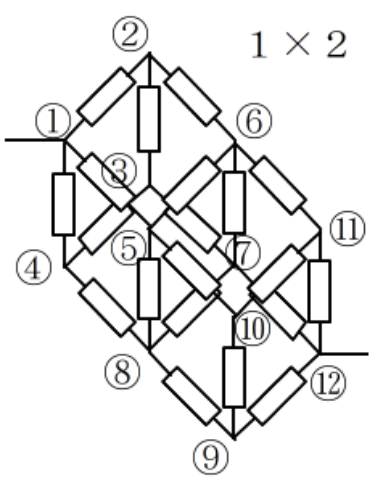
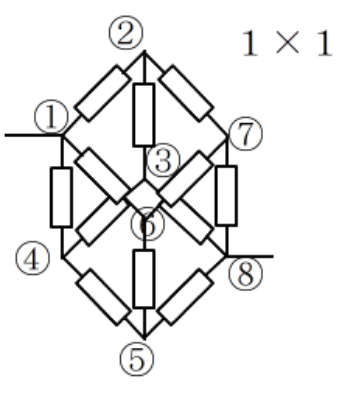
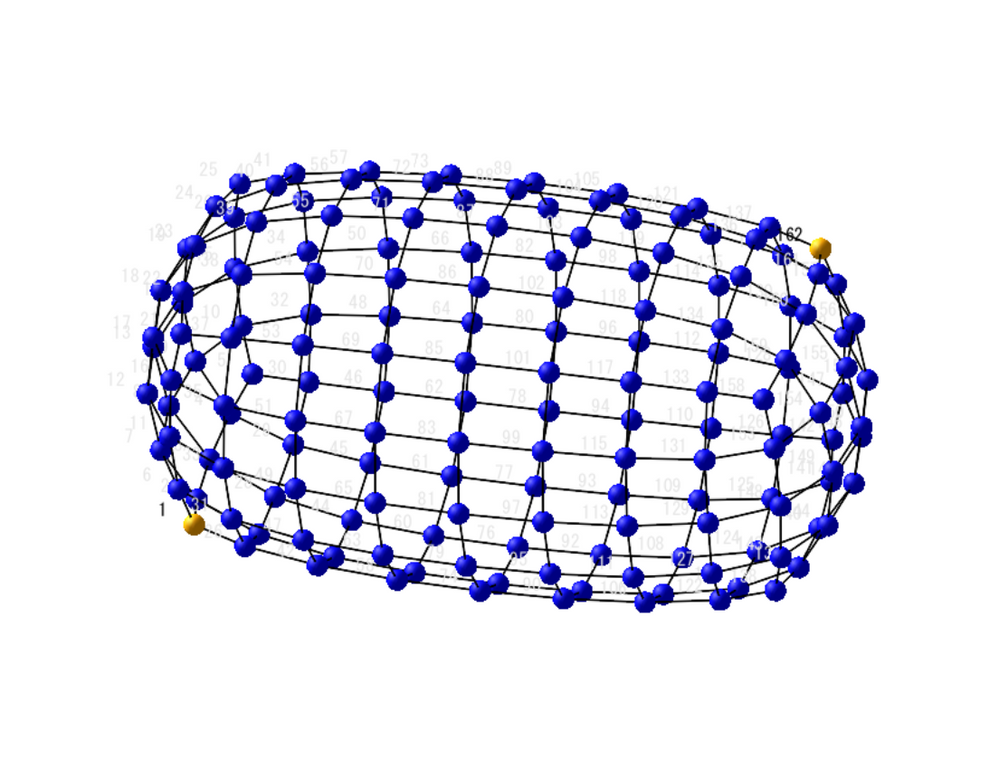
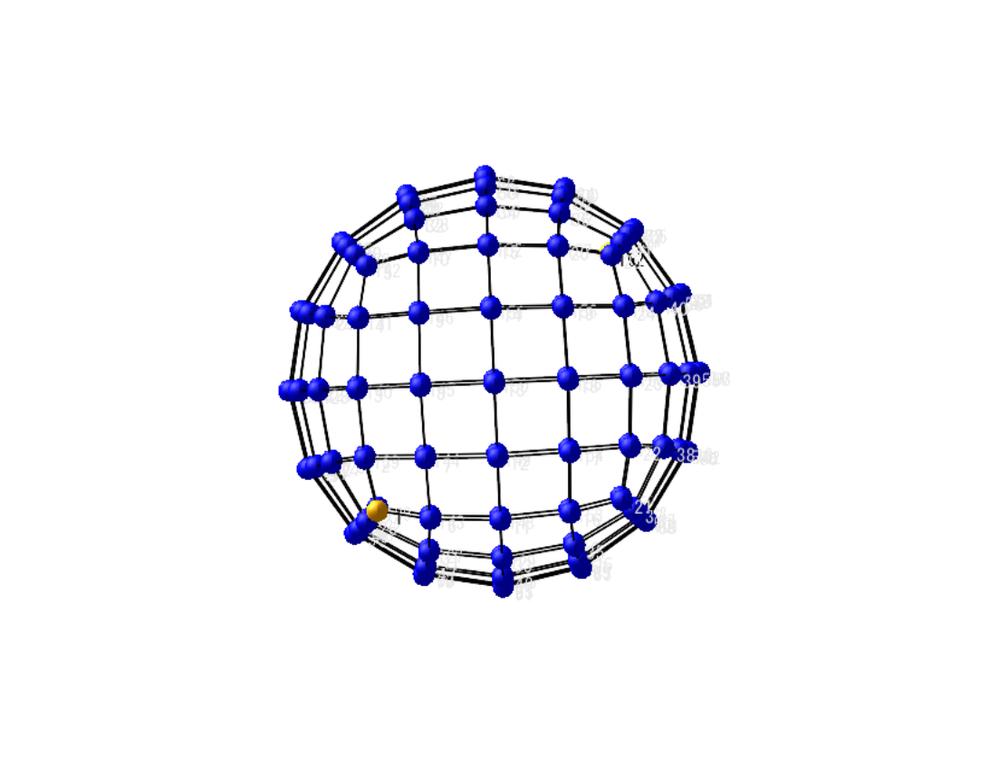
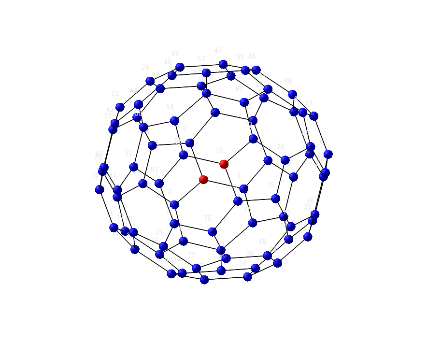
1/3+1/6+1/3 can not use if the grid is 1*1*2. I post many unique resistor grid problems here. This time 60 node soccer ball resistor grid result is shown. Please try to solve it because I can not find any answer in WWW sites. Without using Math software, we can not solve such as R1-2 of resistor ball.
1*1*2 1*1*1
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks.
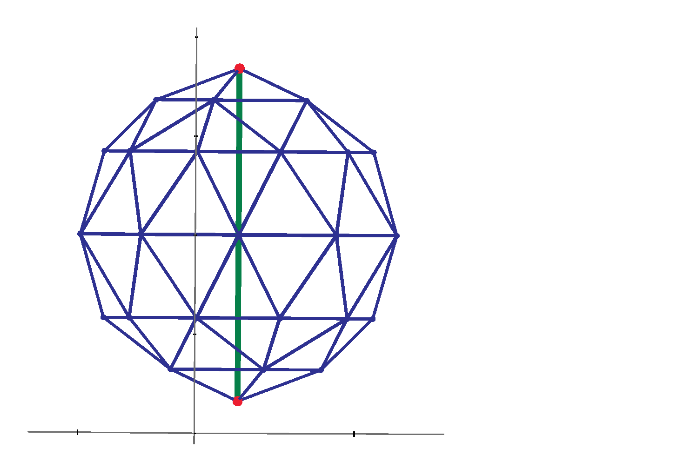
I also find berkeley's PDF from WWW. It shows soccer ball and the introduction to nodal analysis of Electric circuit. All 20th century text books of electric circuit show the principle. However, I can't find the result of node 1 to 31 or node 1 to 2 of soccer ball grid resistor. So I show the results in this post. This electric circuit question must use Mathcad to solve.
This year I check the maple website's Electric circuit examples. These problems shown in maple website are almost as same as text books, therefore, no need to use mathematical tools of 21st century. It is possible to solve even with using pencil and paper.
Tokoro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
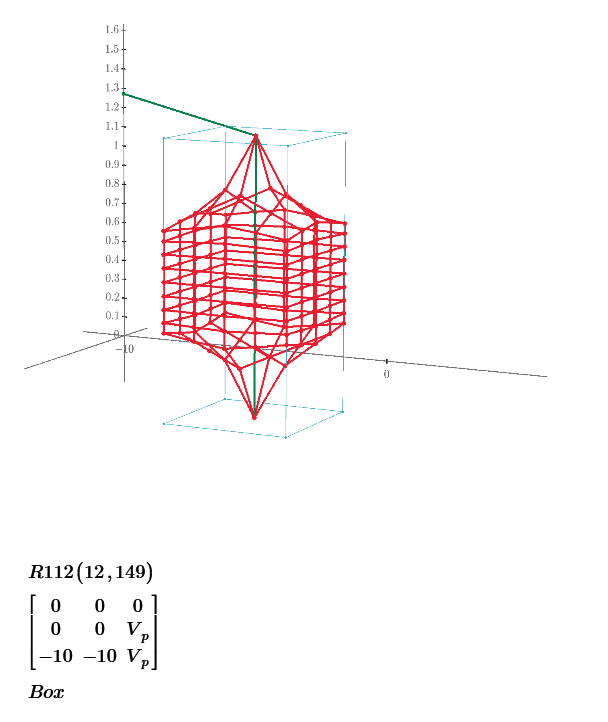
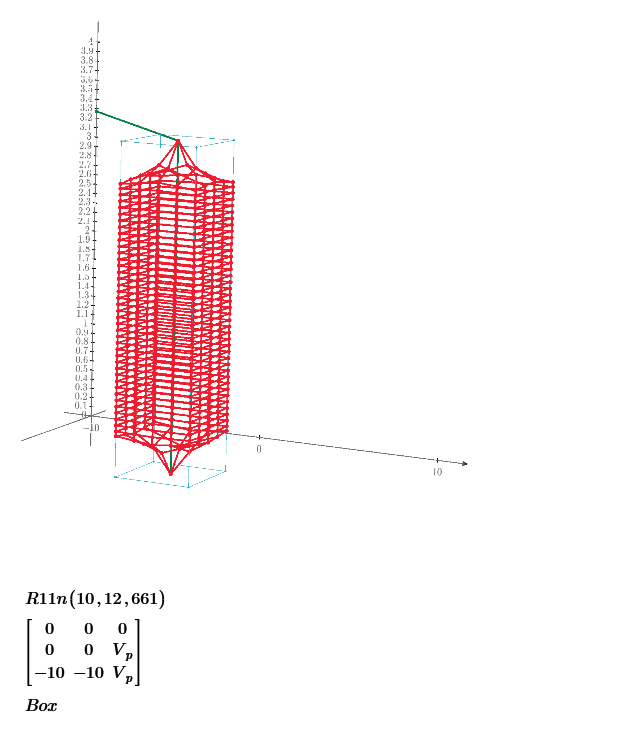
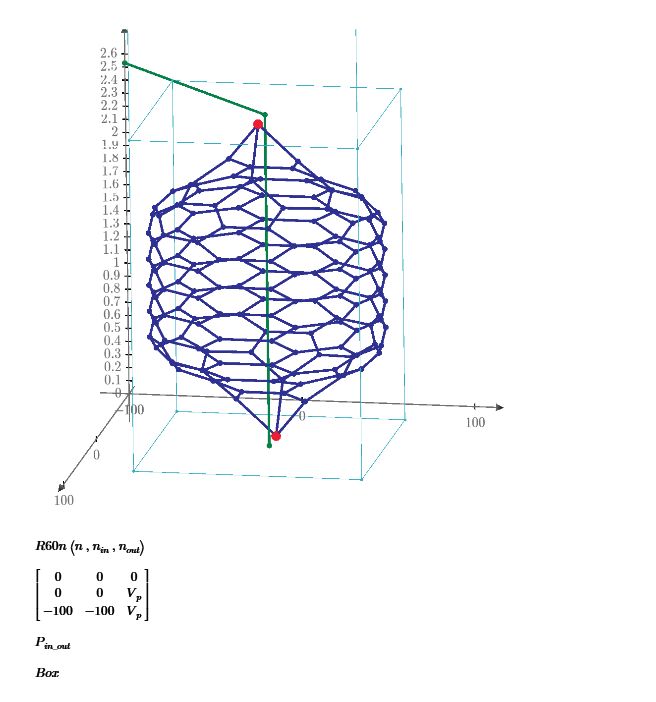
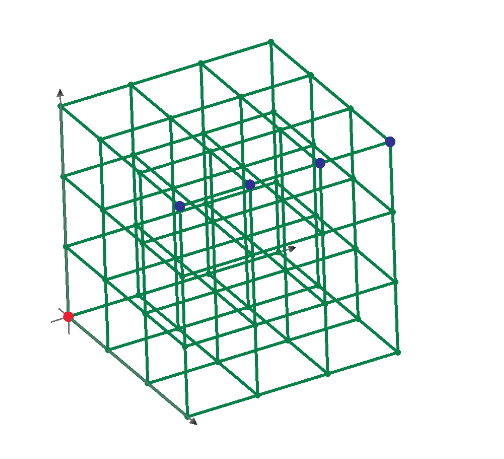
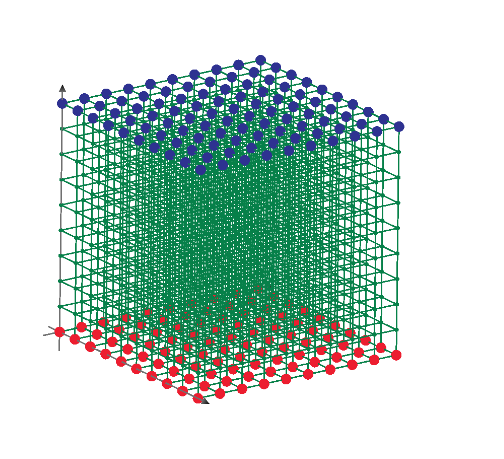
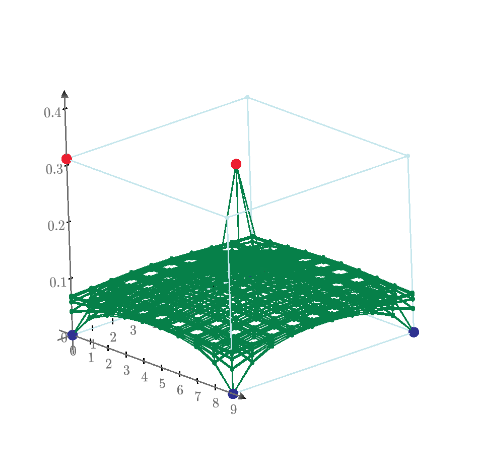
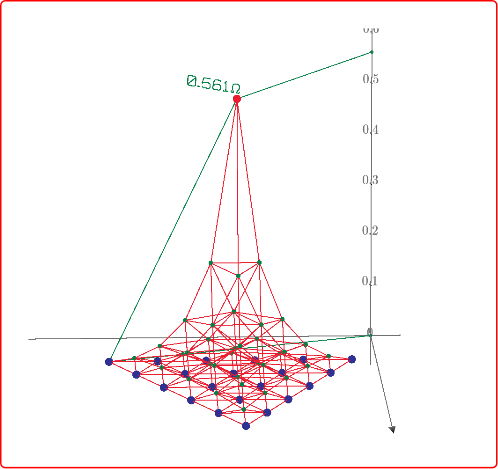
In puzzle 28 of my post, the most far surface distance position from [0,0,0] of 1*1*2 cuboid is [3/4,3/4,2].
So, I make 4 nodes every unit distance and connect each node by 1 ohm to make electric circuit. Only surface of cuboid is meshed by resistors.
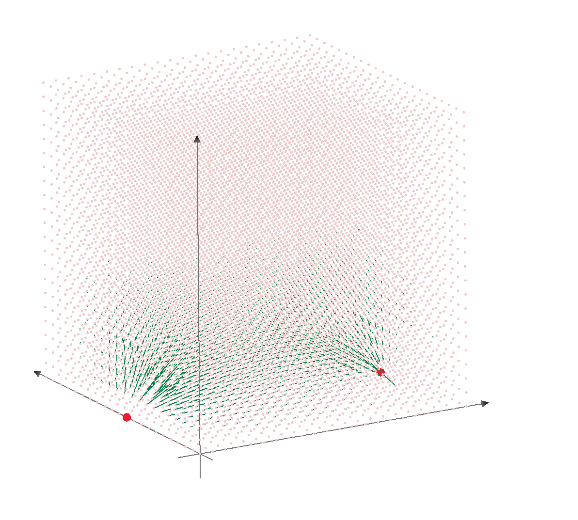
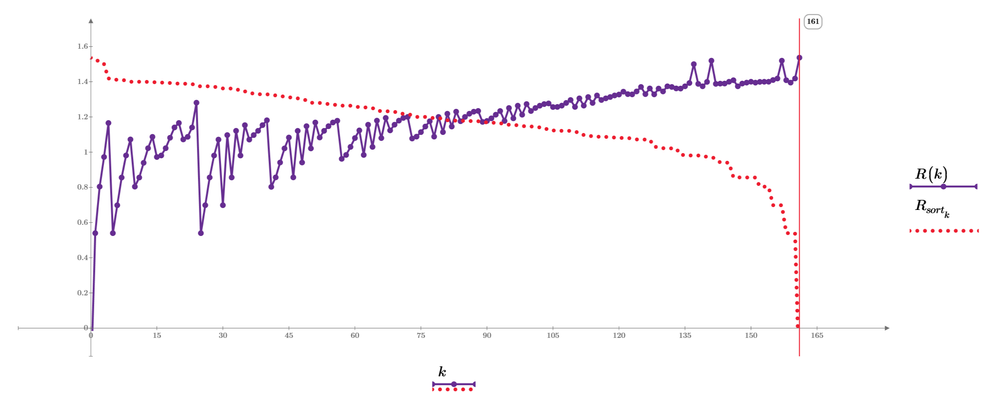
Then measure the resistance from node [0,0,0] to all nodes. Mathcad shows the result as below plot.
Plot says that the largest resistance node is node 161, it is [1*1*2] position and 1.537 ohm.
The resistance between [0,0,0] to [3/4,3/4,2] is node 155 is 1.41 ohm.
The almost most far points of 1*1*2 cuboid are [1/4,1/4,0] to [3/4,3/4,2]. These are node 6 to node 155 of my electric circuit.
And the resistance between these nodes is 1.286 ohm. These results are very interesting.
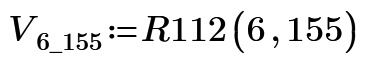
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
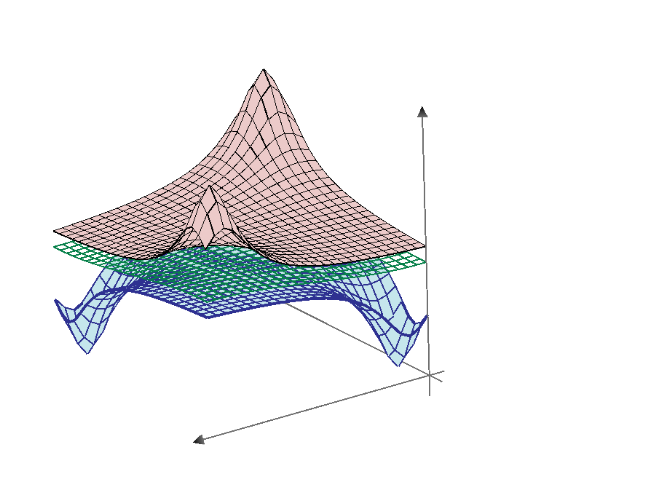
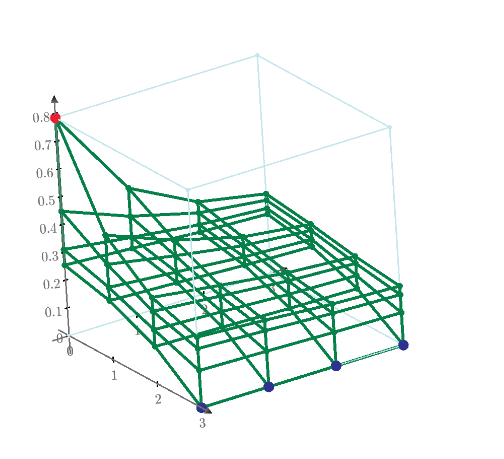
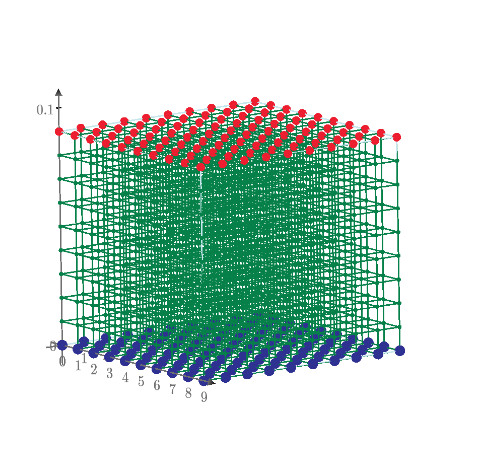
G matrix can plot 3D by maple 2022 graph theory package. And make potential 3D plot by Mathcad Prime.
Z value shows the resistance of node to node.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
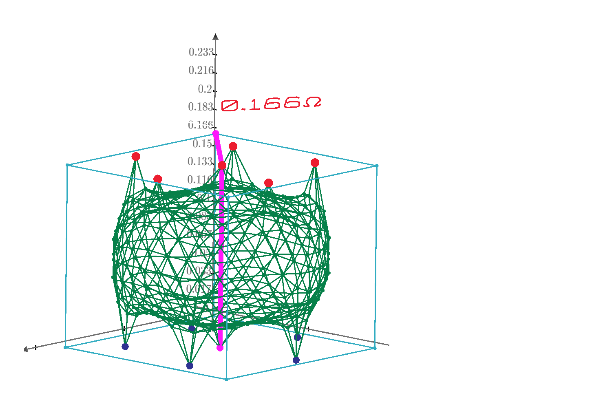
Now, we can show all potential of each node of C60.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
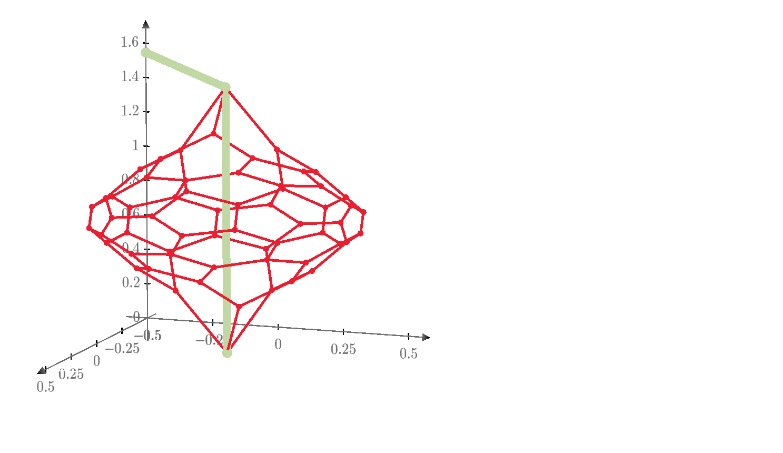
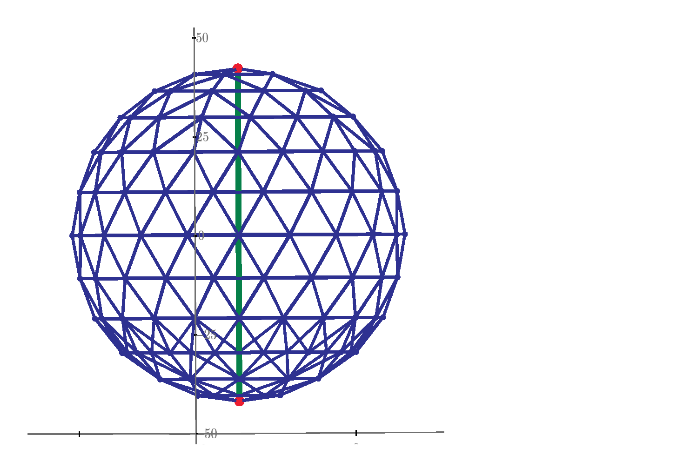
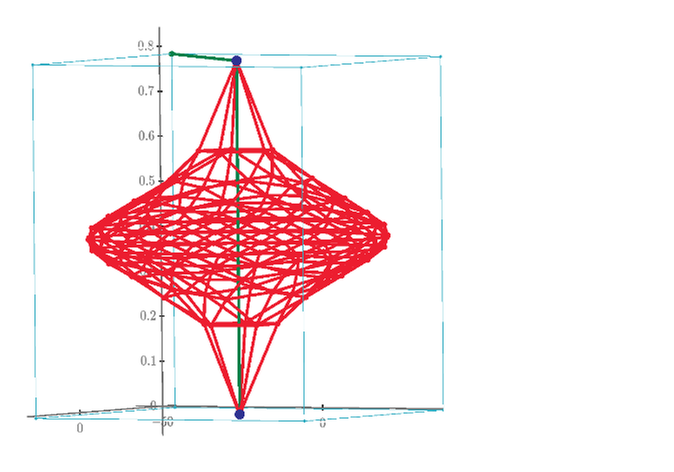
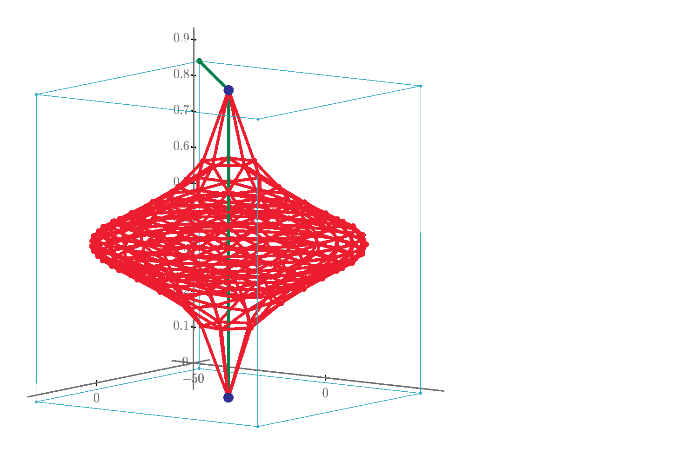
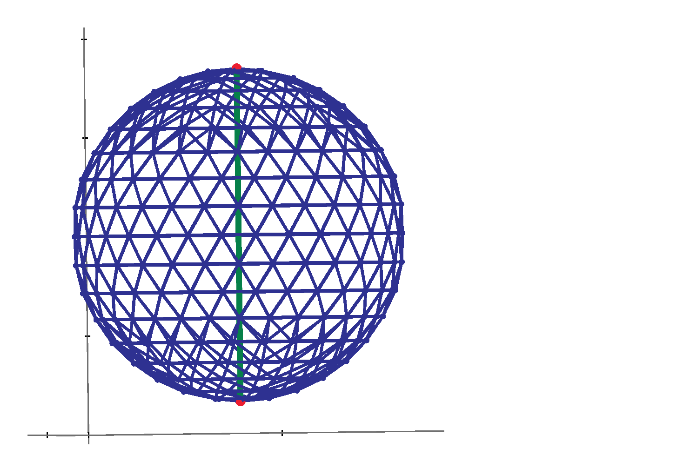
The resistance and voltage distribution of V2 to V6 domes.
Geodesic PVC Sphere Calculator (Mega Hub Connectors) - Sonostarhub
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
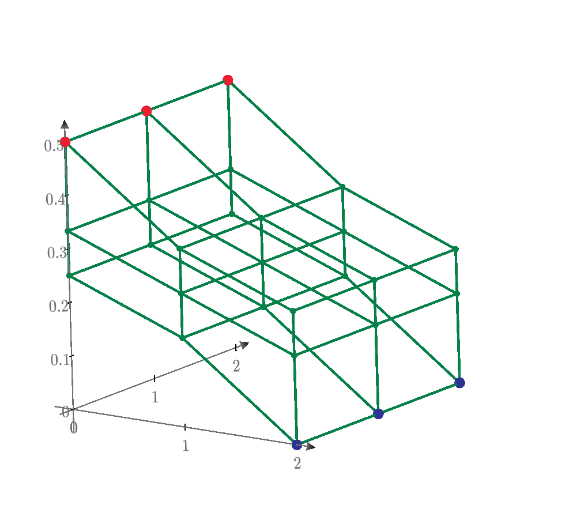
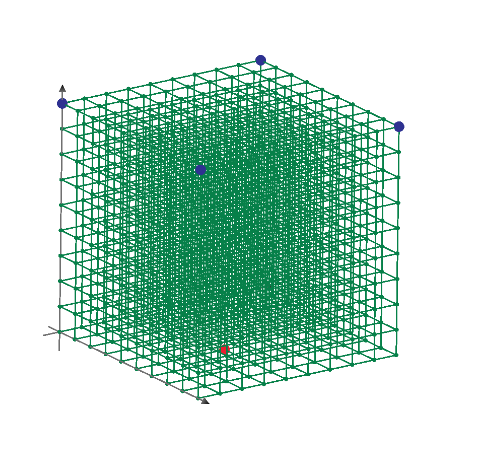
Multi nodes to multi nodes resistance of one ohm mesh circuit. All nodes positions and potencials are plotted.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
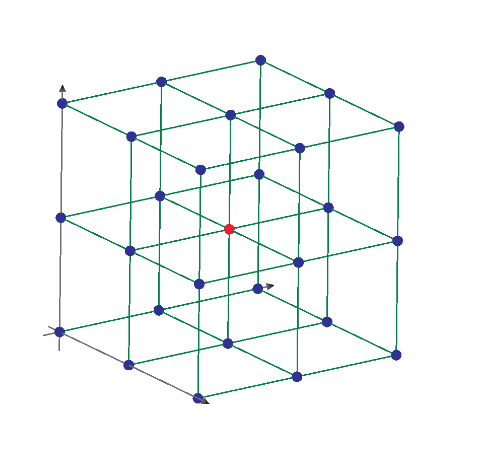
Red points are 1A current sourse applied.
Green points are 1A output nodes.
Orange points are disconnect points.
3D 1 ohm mesh circuit resistance between red and green points is evaluated by using node voltage method.
Any of Blue node to node resistance can change the value, including add the node to node connection.
Blue resistance is changed to 2S from 1S.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
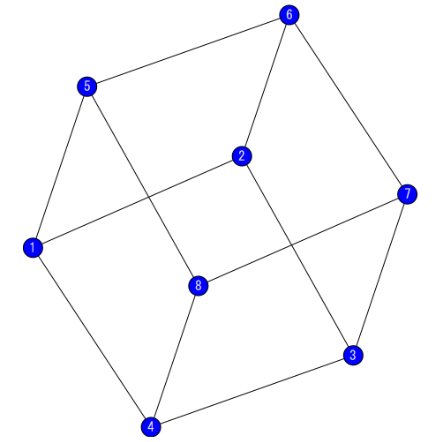
What do you think of my solution? Maybe I took the wrong node as a reference point?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I will check your circuit. Please upload your Mathcad worksheet. I use Prime 9 to solve it.
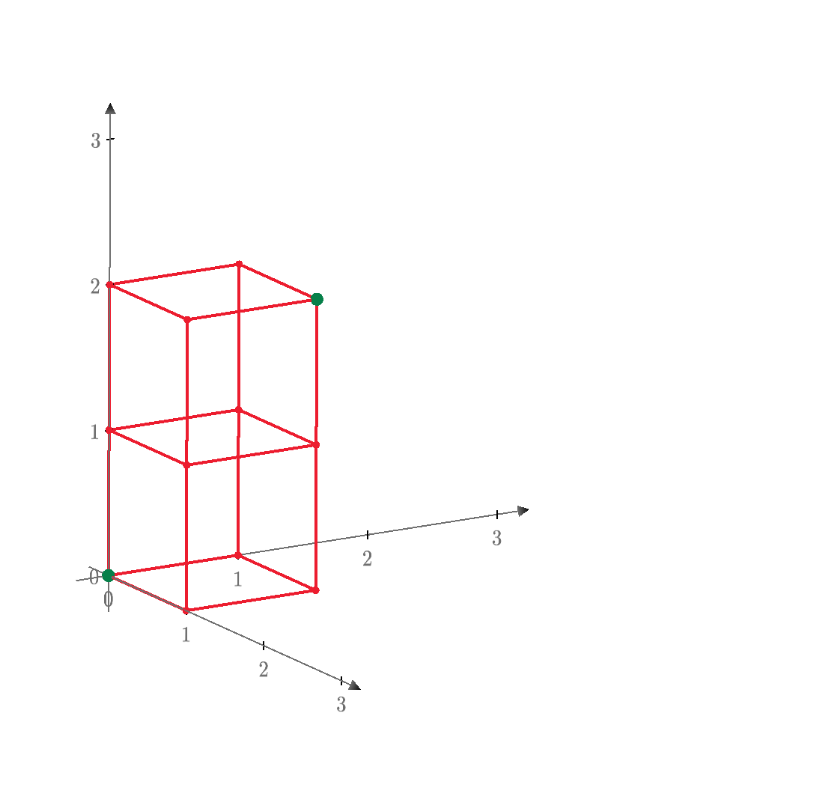
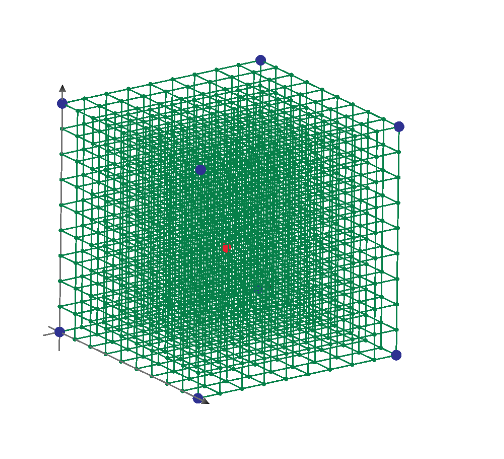
I view your post and I understand this is 3D cube circuit with 12 one ohms to find the equivalent resistance of diagonal nodes. Node method is used to solve the circuit. I think this is the best method to solve the resistance.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
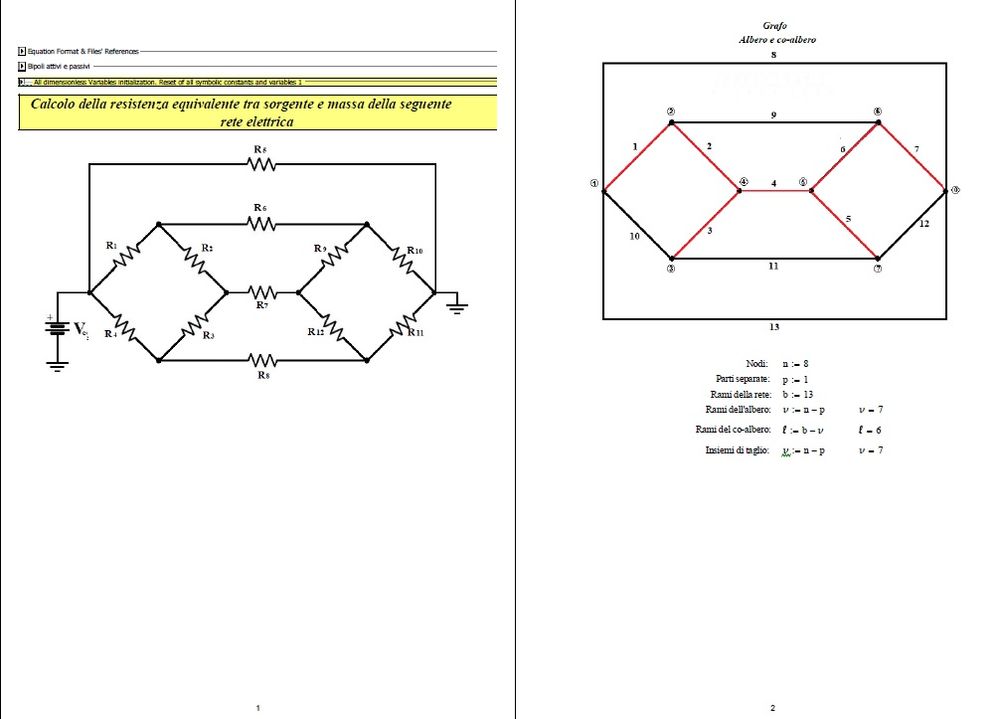
Hi,
Undoubtedly, I made some mistakes. As for the theory, I was inspired by some texts including: "Linesr and non linear circuits" by L. O. Chua, C. A. Desoer, E. S. Kuh, for the construction of the TABLEAU matrix. You can find my worksheet attached.
Greetings
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The correct circuit is this:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
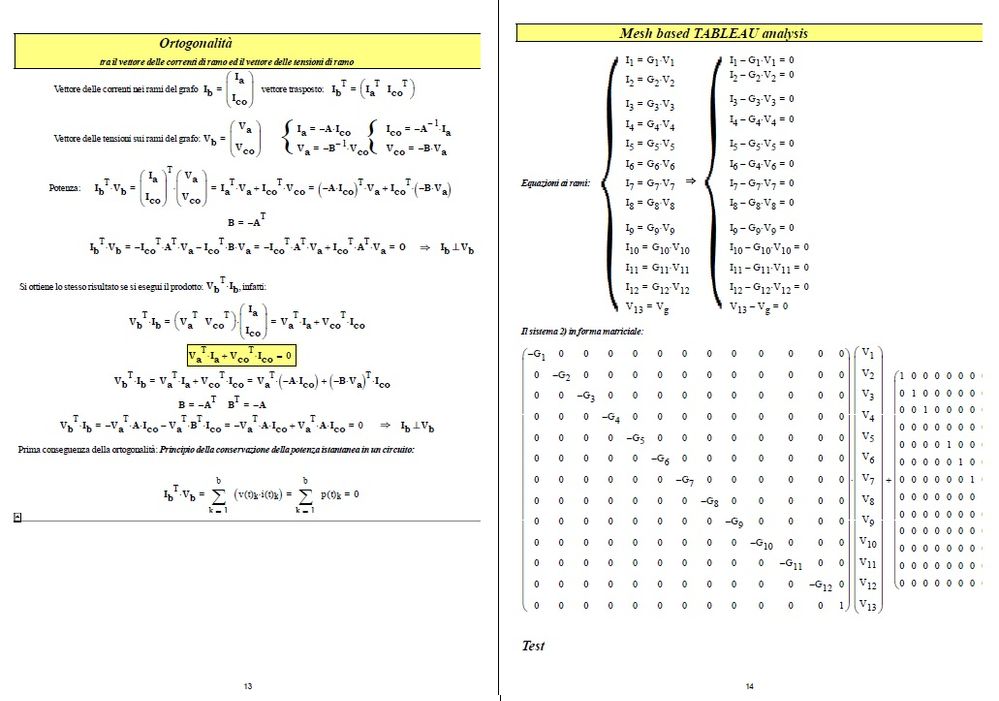
Current vector has +1 and -1 for nodes to evaluate the resistance.
Conductance matrix of earthed node i, g[ii is changed from 3 to 0 is the key of this node method.
We can get all node voltages by lsolve(G,J).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
3.4.5 ohms cube.
1 ohm circuit by 1 ohms. Each 1 ohm has different current when apply 1A for 1 and 13 nodes.
- « Previous
-
- 1
- 2
- Next »