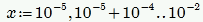Community Tip - Learn all about PTC Community Badges. Engage with PTC and see how many you can earn! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Prime 4.0 Plotting Strangeness
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Prime 4.0 Plotting Strangeness
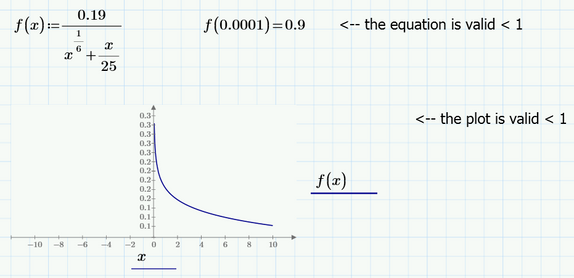
Below is an example of an equation and its respective plot. Everything seems correct and as expected.
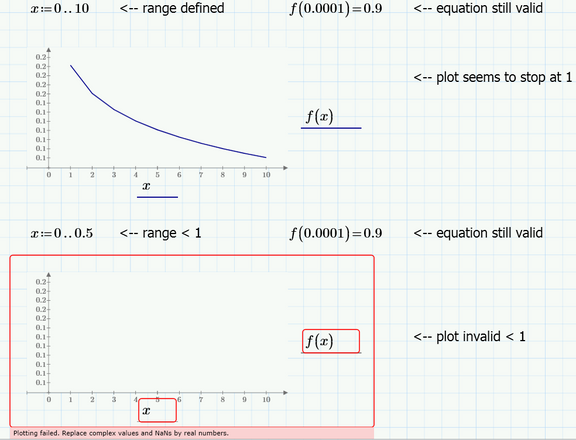
Then I define a range... and the plot stops being valid below 1.
Does anyone have any ideas as to what may be causing such behaviour?
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I don't have MC fired up at the moment to check, but I'm fairly certain your ranges are the problem. Your first range is 0,1,2,3,4,5,6,7,8,10. There is no answer for 0, so it starts at 1. So, graph looks correct.
The next range - I'm not even sure what MC is going to interpret that as. You haven't defined the spacing.
Try this:
x:=0.001,0.002,10
Then you get 0,001, 0.002, 0.003 ..... up to 10. Althought that's a lot of points.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I don't have MC fired up at the moment to check, but I'm fairly certain your ranges are the problem. Your first range is 0,1,2,3,4,5,6,7,8,10. There is no answer for 0, so it starts at 1. So, graph looks correct.
The next range - I'm not even sure what MC is going to interpret that as. You haven't defined the spacing.
Try this:
x:=0.001,0.002,10
Then you get 0,001, 0.002, 0.003 ..... up to 10. Althought that's a lot of points.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks. This solved the problem.
I'm assuming omitting the step size in the range definition fails when the range is below the step size. Is there a way to change the default step size, so that it would be possible to omit it for smaller ranges? (It works fine for large ranges).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Friengineer wrote:
Thanks. This solved the problem.
I'm assuming omitting the step size in the range definition fails when the range is below the step size. Is there a way to change the default step size, so that it would be possible to omit it for smaller ranges? (It works fine for large ranges).
No there is no way to set a default step size - its always 1.
In your first range example you defined the range 0,1,2,3... and because your equation fails a 0, the first point evaluated is at 1 and then at 2 and the two points are connected by a straight line - thats the reason your second plot looks not that smooth and somewhat angular compared to the first one, where you used Mathcads Quickplot feature (letting Mathcad chose a suitable stepwidth).
In your second range you defined 0 .. 0.5. Because of default stepwidth 1 this "range" consists of the number 0 only (the next value 1 being larger than the endvalue 0.5 you provided) and because the plot fails at 0 you get an error.
You are free to chose a range like 0, 0.01 .. 10 even though the plot will fail at 0. it will start at 0.01.
Or, depending on the section you are interested, you may use something like
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Is there a way to change the default step size, so that it would be possible to omit it for smaller ranges?
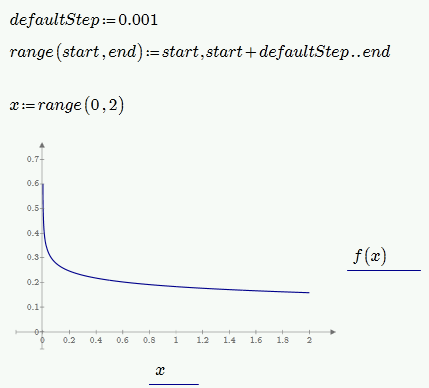
Not out of the box but you can easily create a utility function with a default step width:
But be careful, as Primes 2DPlot (I am not sure if that changed in 4.0 but I don't hink so) has a limit of max. 500001 points it can plot.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you. Much appreciated.
I have another question though:
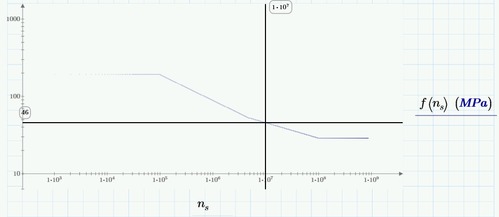
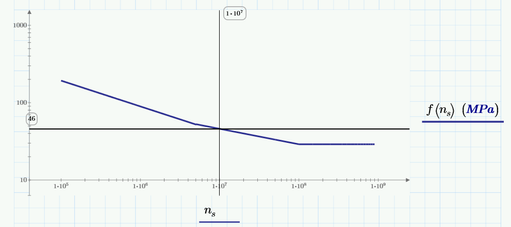
Here's a series of piecewise functions and its plot:
Note how the line is made up of discrete points.
If I change the range to start at the second piecewise function, as follows, the plot becomes a continuous line and I am able to change the thickness settings, etc:
How can I make the first case also generate a solid line?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Scratch that - found the solution:
(Avoid invalid answers and limit no. of points)
Change range to start at 1 and increased step size.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Obviously you ran into one of the limitations of Primes plots.
Your first range consists of 9*10^5 values and this seems to force Prime to plot single unconected points.
Your second range consists of only 9000 values and this works as expected.
Its a nasty limitation and its also a pity that we cannot define a range with logarithmically spaced values.
Two things you may try in such a case:
1) omit the range completely and use Primes Quickplot feature (only possible when the value is unitless). You may have to set the axis limits directly in the plot which is quite uncomfortable as of the tiny font used. You can edit the first, second and last value at each axis.
2) Use logspace to create a vector of logarithmimcally spaced values. Call your function (vectorized) with that vector of values and plot one vector over the other.