Community Tip - You can Bookmark boards, posts or articles that you'd like to access again easily! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Revolved surface using 3D plot
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Revolved surface using 3D plot
Function f(x)=cos(x) x: 0,0.1..2pi
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Please attach your Mathcad sheet, not just a picture.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The 3D plot you show seems not to be from cosine.
Furthermore there are so many ways to rotate cos(x) for x from 0 to 2 pi - vertical axis, horizontal axis ...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
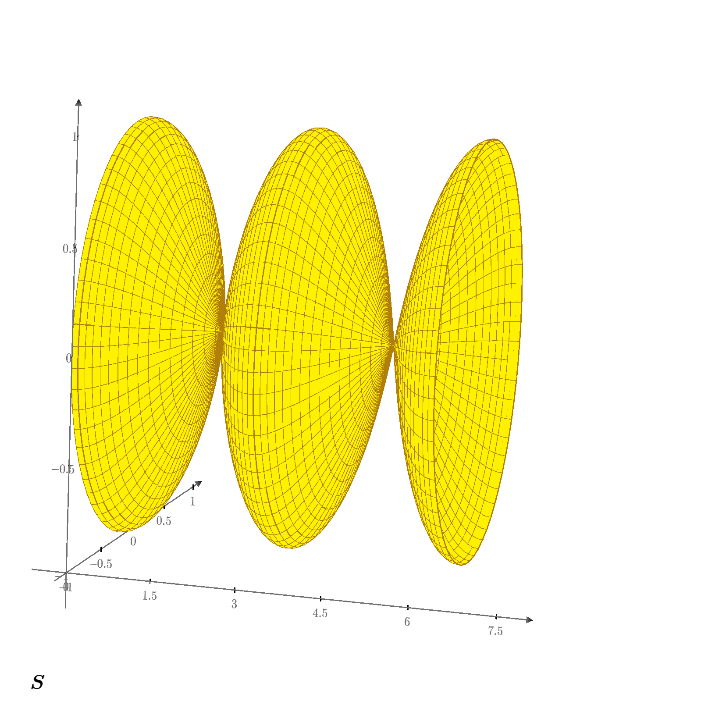
Really appreciate all of your guy's help. Could you please help me to draw this attached shape, which is also shown 3rd shape?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think its better to use the variables you introduced before when creating the mesh
I'd prefer a vector function over three separate ones, but that may be a matter of personal taste.
Its sad that Prime does not offer a way to quickly switch from the bad looking autoscale view
to a more meaningful "equal scale" view. In real Mathcad its just one click. Actually it can be done in Prime, but its a lot of manual work and fumbling around.
Its a pity that PTC is not willing/able to implement a 3D plot which is worth using and would offers at least the formatting abilities we were used from real Mathcad. This sure would still not be state of the art, but at least a huge step forward.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Really appreciate all of your guy's help. Could you please help me to draw this attached shape, which is also shown 3rd shape in our college
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
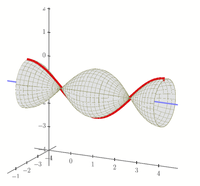
Do you mean that the axis of rotation should be x=-pi ?
At least this is what the picture shows.
It looks to me like it's your homework. Therefore, I think it would be appropriate for you to show a little bit of your own work that goes beyond drawing the cosine function.
You sure will have learned something about how to mathematically represent a surface of revolution, right?
So start with your attempts in a worksheet and post it here if you run into problems.
ttokoro has shown a way how to do the rotation around the x-axis (y=0). You could now start to try to achieve the rotation around the y-axis (x=0) yourself. After that, we will go further and manage the rotation around a parallel to the y-axis, e.g. x=-pi, as shown in the picture.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
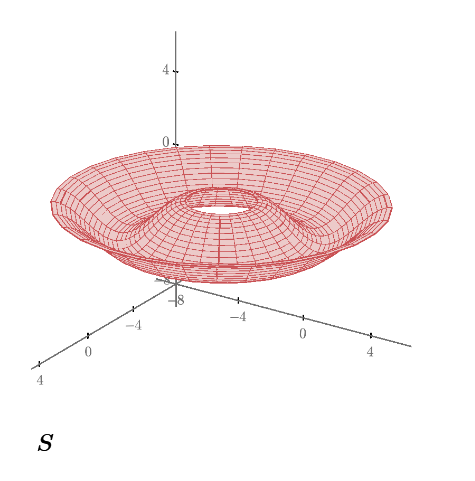
This revolute function is so new to me in Mathcad. these are some samples I used to draw in Solidworks, since I saw it's possible to do this same plot in Mathcad I wanted to try that. In this task, I have drawn my base axis and the shape of the surface. how to make that revolves around that.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
There is no revolute function ore anything like that available in Prime on contrary to Maple, Mathematica, Sage, GeoGebra or others..
Prime allows to make a 3D plot of either three functions in two parameters representing x-, y- and z-value (as was done by ttokoro) or one vector function in two parameters (basically the three functions stacked into one vector. A description how to do that can be found on the Prime help: https://support.ptc.com/help/mathcad/r6.0/de/index.html#page/PTC_Mathcad_Help%2Fcreatespace_and_createmesh.html%23
You did something similar in your file "task ex1" but ended up with a flat space because you had set a to zero.
To rotate a 2D function in x and y around the x- or y-axis you need to formulate that kind of a vector-function or a triple of single functions in 2 parameters yourself. Thats a math problem, not a prime question.
The math necessary can be found in the literature and of course in the net, for example here; https://en.wikipedia.org/wiki/Surface_of_revolution#Coordinate_expressions
So try to use the information there to formulate a function for the surface of rotation with the y-axis as axis of rotation.
After that we can work on the modifications to use an axis not equal but parallel to the y-axis.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Finally got the first one : ) Could you please tell me how did you get the second one.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
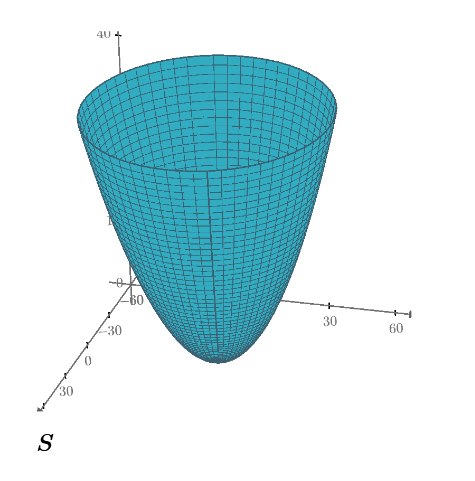
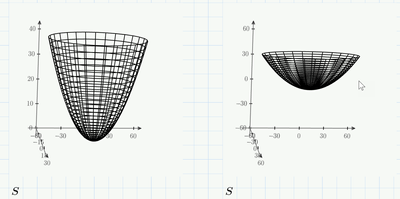
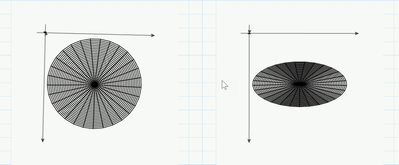
I don't know what the meaning of your "ew 11.mcdx" should be, but you should be aware that in your "tast ex1.mcdx" it is not a surface of revolution which is seen here! Its an elliptic paraboloid. It just looks like a surface of rotation because Prime automatically scales the axis that way and there is no option in Prime to automatically see the object as it really is (equal scale). You would have to manually edit the values for each of the three axis to get the correct view.
See in the pic the comparison - Primes autoscale on the left, manually created equal scale view on the right.
The top view clearly shows that its not a surface created by rotation.
I guess that you just typed in an example you found elsewhere. I can't see any attempt to apply a rotation as e.g. seen in the wikipedia link I posted in my last answer.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator

![16557174892506534801827528554474[1631].jpg 16557174892506534801827528554474[1631].jpg](https://community.ptc.com/t5/image/serverpage/image-id/59016i2E2D441D228557D6/image-size/medium?v=v2&px=400)