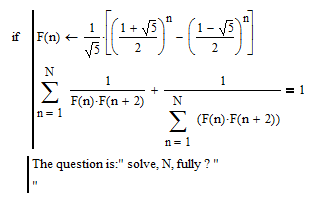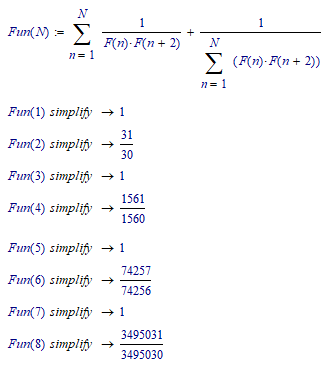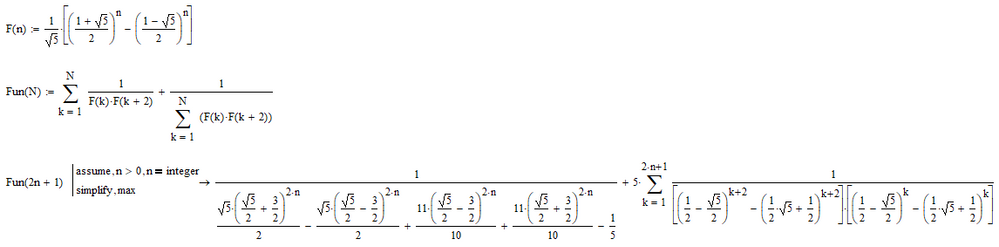Community Tip - Want the oppurtunity to discuss enhancements to PTC products? Join a working group! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
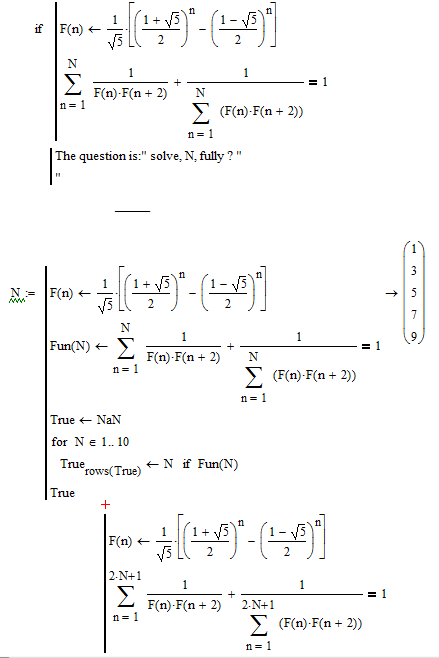
Solve, N, fully ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Solve, N, fully ?
Hi, Everyone.
From the following:
How to solve, N, fully (the above) ?
Thanks in advance for your time and help.
Best Regards.
Loi.
Solved! Go to Solution.
- Labels:
-
Math Homework
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I'd say: Fun(N)=1, solve, N, fully
should give: N is odd.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Isn't the solution N = infinite ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I'd say: Fun(N)=1, solve, N, fully
should give: N is odd.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@LucMeekes wrote:
I'd say: Fun(N)=1, solve, N, fully
should give: N is odd.
I agree. My assumption N=infinity was grossly incomplete 😉
Is Maple in MC11 able to prove it? muPad in MC15 isn't:
Problem is the first summand in Fun(N) (Mathcad changes the order in the result) as already seen here: https://community.ptc.com/t5/Mathcad/Sum-of-reciprocals/m-p/827578/highlight/true#M202986
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Note that you should not assume n>0, since n=0 gives 2*n+1=1, the first odd number.
Can maple prove it?
Let's try:
That's equivalent to MuPad's result. Setting n to a n integer:
The command simplify:
Doesn't simplify, but simplify, max:
creates a different result, I've never seen simplify, max create a different result from simply simplify in Mathcad 11.
But then again, simplify, simpler creates that very same result:
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In MC14/15 "simplify,max" often makes a difference, but apart from taking much more time it also sometimes returns a result which is even worse compared to the one we get with "simplify" alone.
BTW, "simplify,simpler" throws the error "Modifier is unknown or not allowed here" in MC15.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mathcad 11 doesn't know that error message. It allows anything as a modifier for simplify. But it's striking to see that an absent modifier gives a (slightly but) different result from a non-empty modifier.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Many thanks, Luc and Werner.
Luc, with your suggestion above, And I agree with you, too:
Best Regards.
Loi.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is a list for the first few N showing N, the reduced first an second summand and the complete sum.
Some sort of pattern can be seen, but the proof is .... ??