Community Tip - Have a PTC product question you need answered fast? Chances are someone has asked it before. Learn about the community search. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
sum several sin
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
sum several sin
Hi All,
I have a problem. Here I discribe the case.
A triplex plunger pump will produce water hammer. This will create a sinus wave, by opening the inletvalve and closing the inletvalve. I have 3 plunjers so 6 vibration sinus.
I like to sum these sinus. See my enclosed worksheet.
by calculating with my hand calculator I get an answer. In mathcad I get only 'zero' (0). What do I wrong.
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Your sheet is correct. Mathcad has tolerances for numbers close to zero being displayed as zero. If you change these values (format/results/tolerances, you get very small numbers. If you calculate y for various values of alpha, you can see that the summation is always very small.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Terms 1, 2, and 3 sum to zero. So do terms 4, 5, and 6. This is true for all values of alpha, alpha2, and beta.
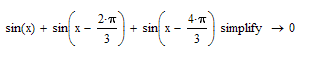
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Your sheet is correct. Mathcad has tolerances for numbers close to zero being displayed as zero. If you change these values (format/results/tolerances, you get very small numbers. If you calculate y for various values of alpha, you can see that the summation is always very small.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fred Kohlhepp wrote:
Your sheet is correct. Mathcad has tolerances for numbers close to zero being displayed as zero. If you change these values (format/results/tolerances, you get very small numbers. If you calculate y for various values of alpha, you can see that the summation is always very small.
Yes, but these are roundoff errors. As Richard had shown the sum should always total to a perfect zero as in every of the two sets of three sines they are phase shifted by exactly 1/3 od their period!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Mr. Kohlhepp, I will study what you have done!
Regards,
Peter
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You are adding three sinusoids of equal amplitude that are phase shifted by 1/3 of their period. Apart from numeric round off error they add to zero. Always. The values of alpha, alpha2, and beta do not matter. This is a mathematical certainty, and the worksheet therefore tells you nothing about your pump. Whatever you calculated using your hand calculator, it was not this (whether by design or by mistake).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Dear Mr. Jackson,
You are partly right. I try to explain where I am looking for.
The plungerpump where are using, creates a visual vibrition in the suctionline. The company I am working for, uses this pump for over 12 years. The last 6 months we have problems with vibration. There are a number of changes made in the design, (all the designs are custom build).
For 12 years PVC is used, the manufacturer of PVC is changed. The PVC components are not from the same manufacturer as the pipe. Because of reducing costs, the rpm of the pump is rised, pipe diameters are down sided. The pipe diameters are not downsided anymore.
What do I have found:
1. The pump has 3 plungers, so 3 inlet valves. 795 rpm = 13.25 Hz.
2. Total time for 180 degrees of travel of the plunger is about 0.03774 sec
3. Each inlet valve opens and closed within the critical time (about 3 msec) of water hamer. -> 6 sinusoids
4. Inlet pressure is 1.5 bar, discharge pressure 68 bar max (both relative). Between the inlet valve and plunger there is a champer and between the outlet valve and plunger there is an other chamber (dimensions scaled from photo) -> Inlet valve 1 opens on 5.191deg (first sinusoid) and closes 186.16x deg (forth sinusoid). I assume that every plunger starts 120 deg later (not messured)! The inlet valve is always between 180.161 and 180.163 deg open.
5. There are moments that 1 inlet valve or 2 inlet valves are opened on the same time. By that the suction volume is not constant and fluactute the pressure a little.
6. Water hamer does the following:
6a. It creates a sinusoid wave with the speed of sound (water between 1400 m/s and 1500 m/s). The wave is traveling away from the pump. The flow to the pump is fully stopped. If the wave is returning the flow to the pump will start again.
6b. The water hammer wave will increase the pressure, you can calculate that (for example Georg Fischer) during running away from the pump
6c. The water hammer wave will descrease in amplitude by resistance, expansion of piping etc.
6d. The flow to the pump stops, will increase pressure
6e. Because a large tank is in the suctionline mounted (2 mWc) , the fluid will flow to the pump again.
6f. The water hammer wave will stop a the large tank and returning to direction of the pump. This will boost the fluid more to the pump (amplitude is decreased, see 6c)
6g. Supporting is not enough. I have found a Belgium University Essay (Dutch) where the calculation of supporting can be calculated.
6h. Check in practice by expirementing several solutions and check calculations.
The reason of the calculation is as follows:
1. understand what is happing
2. predict what is required to make a vibration acceptable suctionline
Regards,
Peter
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for the explanation of what you are trying to do. My point though is that the worksheet you posted does not help you to do that. The sum of six sinusoids, as presented, is identically zero. You can make your three parameters anything you want. The sum will always be zero (to within numeric roundoff errors), so it can tell you nothing abut any real world system.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Dear Mr. Jackson,
Thank you for the explanation. One step I have to make, is slowly lower the amplitute of the sinusoid. The lowering of amplitute is caused by internal friction of fluid and piping, expanding piping, litte compressing the volume of the fluid. This will give a damping vibration wave.
I have found a formula which is calculating the pressure rise caused by water hammer. Never found the explanation how they get the formula.
Before I started I have read quit a lot about the subject, never a solution for a plunger pump seen.
Maybe I am on the wrong way.
Regards,
Peter
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Water hammer is, as you say, caused by the sudden change in pressure due to the opening or closing of a valve. This causes a compression (shock) or expansion wave to travel away from the source at the speed of sound. The usual cure is a properly sized and carefully placed accumulator. The problem is also common in hydraulic power systems.
Taken from a discussion about plunger pumps:
AFFINITY
Although we tend to associate affinity laws with centrifugal pumps, other mechanical devices also exhibit these “ natural” relationships. In the case of positive displacement pumps the affinity laws are very straight forward.
Flow - Flow varies directly with a change in speed. If the rotational speed is doubled, flow is also doubled.
Pressure - Pressure is independent of a change in speed. If we ignore efficiency losses, the pressure generated at any given rotational speed will be that required to support flow.
Horsepower - Horsepower varies directly with a change in speed. If we double the rotational speed, twice as much power will be required.
NPSHr - Net Positive Suction Head required varies as the square of a change in speed. If we double the rotational speed NPSHR increases by four.
You noted that the pipe size got smaller and the pump speed increased. Both of those effects would raise the discharge pressure. Perhaps of more concern is the statementy about suction head. Increasing the pump speed also raises the required pressure at the pump inlet. If you have not increased that, might you be cavitating in the pump?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Dear Mr. Kohlhepp,
Thank you for the article. I will look if I can find it.
Regards,
Peter





